Распределение ущерба

На практике важно учесть обе характеристики величины риска – частоту (вероятность) возникновения и размер (тяжесть) ущерба. Их совместное рассмотрение позволит глубже проанализировать количественные аспекты исследуемых рисков, а также сформировать набор более эффективных мероприятий по управлению риском.

В основе такого подхода лежит тот факт, что частота возникновения и размер (тяжесть) ущерба не проявляются независимо. Действительно, для убытков определенной величины характерна определенная частота (вероятность) их возникновения. Такая взаимосвязь носит название распределения ущерба. Его можно выразить в аналитической или графической форме. Один из вариантов подобного графического представления (плотность распределения ущерба) приведен на рис. 2.1.

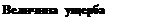
Рис. 2.1. Плотность распределения ущерба

Кривая, изображенная на рис. 2.1, более или менее типична: как правило, катастрофические убытки характеризуются очень маленькими вероятностями их реализации, так что правый «хвост» распределения убывает достаточно медленно. В большинстве случаев можно выделить наиболее вероятный ущерб, соответствующий максимуму плотности распределения (как это показано на рис. 2.1). Однако иногда вероятность убытков регулярно уменьшается с ростом их размера, так что оценить наиболее вероятный ущерб невозможно.

Форма зависимости, приведенная на рис. 2.1, характерна для ситуаций, когда величина ущерба может изменяться непрерывно. Если же подобные изменения могут быть только дискретными или имеется информация лишь об интервалах значений размера убытков, то график будет представлять собой столбиковую диаграмму. В целом для каждого конкретного риска характерно свое специфическое распределение, изучение особенностей которого очень важно для оценки и анализа рисков.

Распределения используются в рамках теории вероятностей для описания случайных величин, которые в связи с этим являются удобной моделью рисков. Применение таких моделей позволяет использовать мощный математический аппарат для анализа системы управления риском. Помимо исследования формы зависимостей между величинами ущерба и вероятностями их реализации, на их основе рассчитываются и анализируются следующие специальные числовые характеристики:

- характеристики положения, т.е. показатели, некоторым образом описывающие центр распределения, вокруг которого колеблются возможные значения ущерба (математическое ожидание, медиана, мода и т.п.);

- характеристики рассеяния, т.е. величины, определяющие степень разброса возможных убытков (дисперсия, стандартное отклонение, коэффициент вариации, интерквартильное расстояние и т.д.).

С одной стороны, такие показатели чрезвычайно важны для анализа рисков как инструмент их измерения и сравнения. С другой стороны, по их численным значениям можно проводить дополнительную классификацию анализируемых рисков.

Для оценки конкретного вида распределений ущерба используется статистика убытков по реальным рискам. Как подчеркивалось в предыдущем параграфе, дефицит подобной информации и степень ее достоверности могут существенно повлиять на точность анализа рисков.

Если данных для численной оценки распределения недостаточно, то, используя экспертную информацию, можно хотя бы провести совместную классификацию по размеру ущерба и частоте его возникновения (табл. 2.1).

Такая классификация позволяет понять специфику различных рисков. Очевидно, что для рисков, выделенных в соответствии с данной классификацией, методы управления будут совершенно различны.

Таблица 2.1