Задание 23

Вопрос 1. Сколько систем частных решений образуют фундаментальную систему решений системы трех линейных однородных дифференциальных уравнений с постоянными коэффициентами?

1. 1

2. 2

3. 3

4. 4

5. Фундаментальную систему образует одно общее решение системы

Вопрос 2. При каком условии может быть получено частное решение системы линейных однородных дифференциальных уравнений с постоянными коэффициентами, удовлетворяющее любым заданным начальным условиям?

1. Наличие фундаментальной системы решений

2. Непрерывность функций, образующих некоторое частное решение

3. Интегрируемость функций, образующих общее решение

4. Определитель матрицы, строками которой являются частные решения системы дифференциальных уравнений при не обращается в ноль

5. Определитель матрицы, строками которой являются частные решения системы дифференциальных уравнений равен нулю

Вопрос 3. Какой вид имеет частное решение системы линейных однородных дифференциальных уравнений с постоянными коэффициентами в случае действительных и различных корней характеристического уравнения ?

1.

2.

3. , где - постоянные величины

4. , где - постоянные величины

5. Здесь нет частного решения

Вопрос 4. Какой вид имеет частное решение системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами в случае комплексных корней характеристического уравнения ?

1. , где - постоянные величины

2. , где - постоянные величины

3.

4. , где - постоянные величины

5. 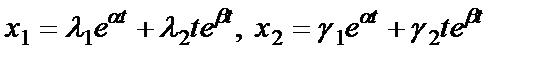, где - постоянные величины