ПЕРЕВОД ИЗ ЛЮБОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ.

Перевод чисел из любой системы счислению в десятичную в целом гораздо проще, чем перевод из десятичной любую. Перевод этот основан на полиномиальной записи числа. Чтобы понять, что это такое, вернёмся к разделу «цифры и числа». Там мы рассматривали такую картинку:

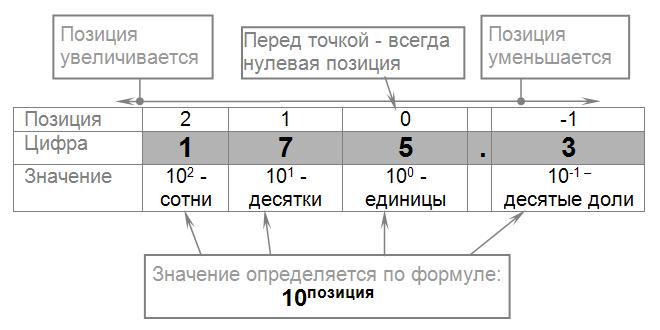
Если взять каждую цифру и умножить её на множитель, соответствующий позиции, то получится полиномиальная запись числа:

1*10²+7*10¹+5*⁰+3*^-1=175.3

Фактически мы имеем обычный полином. Значение этого полинома можно посчитать. В данном случае, поскольку мы в полиномиальной форме записали десятичное число - то можно сказать, что мы перевели число из десятичной системы счисления в десятичную - естественно при этом получили само это число.

А теперь самое интересное - эта полиномиальная запись числа может использоваться для перевода из любой системы счисления в десятичную. Фактически, в разделе «цифры и числа» мы выполнили такой перевод несколько раз - если Вы этого не заметили, пересмотрите этот раздел ещё раз и найдите, где был выполнен такой перевод.

Вот ещё один пример перевода числа из шестнадцатеричной системы счисления в десятичную:

4E7F.3F1₁₆= 4*16³ + 14*16² + 7*16¹ + 15*16⁰ + 3*16^-1 + 15*16^-2 + 1*16^-3=
16384 + 3584 + 112 + 15 + 0.1875 + 0.05859375 + 0.000244140625 = 20095.246337890625₁₀

Обратите внимание, что перевод осуществляется в десятичную систему счисления за счёт того, что все операции (возведение в степень, умножение, сложение) выполняются в десятичной системе счисления. Если бы мы с такой же лёгкостью выполняли эти операции в любой другой системе счисления, то этот способ можно было бы использовать для перевода чисел из любой системы счисления в любую другую.

Например, при использовании этого способа для перевода в восьмеричную систему счисления, перевод будет выглядеть так:

4E7F.3F1₁₆= 4*20³ + 16*20² + 7*20¹ + 17*20⁰ + 3*20^-1 + 17*20^-2 + 1*20^-3=
4*10000 + 16*400 + 7*20 + 17 + 3*0.04 + 17*0.002 + 1*0.0001 =
40000 + 7000 + 160 + 17 + 0.14 + 0.036 + 0.0001 = 47177.1761₈

В данном случае все операции выполняются в восьмеричной системе счисления.

Например, 7*20=160₈ (а не привычное нам 140₁₀) - потому что операции выполняются в восьмеричной системе счисления вместо привычной нам десятичной. 20₈ - это те же 16₁₀, которые мы возводили в степень при переводе в десятичную систему счисления. Если перевести все числа в десятичную систему счисления, то это умножение будет выглядеть так: 7*16=112₁₀- то есть в точности то же самое, что мы имели при переводе этого числа в десятичную систему счисления.