
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ВЫСКАЗЫВАНИЯ-ПРОСТЫЕ И СОСТАВНЫЕ. ЛОГИЧЕСКИЕ СВЯЗКИ.
С грамматической точки зрения, высказывание – это повествовательное предложение.
Сложные предложения строятся из выражений, обозначающих некоторые понятия, и логических связок. Слова и обороты НЕ, И, ИЛИ, ЕСЛИ … ТО, ТОГДА И ТОЛЬКО ТОГДА, СУЩЕСТВУЕТ, ВСЕ и некоторые другие называются логическими связками (операторами) и обозначают логические операции, с помощью которых из одних предложений строятся другие.
Предложения без логических связок являются элементарными, их нельзя расчленить на части так, чтобы при этом каждая из частей была также предложением. Элементарные высказывания называются также высказываниями (суждениями). В высказываниях содержится информация о предметах, явлениях, процессах.
Элементарное высказывание состоит из субъекта (логического подлежащего) – того, о чем идет речь в высказывании, и предиката (логического сказуемого) – того, что утверждается или отрицается в высказывании о субъекте.
Таким образом, высказывание – это форма мышления, в которой утверждается или отрицается логическая связь между понятиями, выступающими в качестве субъекта и предиката данного высказывания. Соответствие или несоответствие этой связи реальности делает высказывание (суждение) истинным или ложным.
Логическая связь между субъектом и предикатом высказывания выражается обычно в виде связки ЕСТЬ или НЕ ЕСТЬ, хотя в самом предложении эта связка может отсутствовать, а лишь подразумеваться. При этом субъект высказывания может выражаться не обязательно только подлежащим в предложении, так же как и предикат – не только сказуемым (это могут быть и другие члены предложения). Что считать в предложении субъектом, а что предикатом высказывания определяется логическимударением. Логическое ударение связано со смыслом, содержащимся в предложении для говорящего или слушающего.
По форме высказывания делятся на простые (имеющие логическую форму «S есть P» или «S не есть P», где S – субъект, P – предикат) и сложные (грамматически выражающиеся сложными предложениями).
Пример простого высказывания: «Все медведи любят мед», сложного – «Некоторые медведи любят мед и молодые побеги бамбука».
Простые высказывания позволяют выразить следующие типы высказываний:
· атрибутивные высказывания – выражают принадлежность или не принадлежность свойства объекту или классу (например, Земля есть планета);
· высказывания об отношениях– говорят о наличии отношения между объектами (например, 3<5);
· высказывания существования (экзистенциональные высказывания)– говорят о существовании или не существовании объекта или явления.
Операции на множестве высказываний.
Из элементарных высказываний можно составлять сложные высказывания с помощью логических операций. Элементарные высказывания, входящие в состав сложного высказывания, связываются логическими операторами не по смысловому описанию, а только по их истинностным значениям. Следовательно, сложные высказывания являются функциями от входящих в них элементарных высказываний. Все операции в логике высказываний описываются только таблицей истинности.
К операциям на множестве высказываний относятся:
· Отрицание. Для него таблица истинности:

| 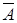
|
Иллюстрацией отрицания в естественном языке служит частица "не", или слова "неверно, что".
· Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны. Эту логическую операцию называется еще логическим умножением, или логическим минимумом. Выпишем таблицу истинности для конъюнкции

| 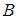
| 
|
В естественном языке она чаще всего интерпретируется союзом «и».
· Дизъюнкция двух элементарных высказываний истинна тогда и только тогда, когда истинно хотя бы одно из элементарных высказываний. Ее иногда называется логическим сложением или логическим максимумом. Таблица истинности дизъюнкции выглядит так:

| 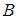
| 
|
Определение конъюнкции и дизъюнкции распространяется на любое число высказываний.
· Стрелка Пирса задается следующей таблицей истинности:

| 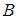
| 
|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
· Операция «исключающего или» задается следующей таблицей истинности, она истинна, когда истинен только один из операндов. Эту операцию еще называют строгой дизъюнкцией или логическим неравенством.

| 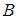
| 
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
В языковом эквиваленте чаще всего эта операция выражается сложным союзом «либо , либо ».
· Импликация выражение читается так: «если , то»

| 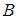
| 
|
В таком виде часто формулируются математические теоремы. Если теорема сформулирована как-нибудь иначе, то ее можно перефразировать в указанном виде, не теряя её сущности.
· Эквивалентность еще иногда называют логическим равенством.

| 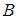
| 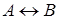
|
В математических терминах эта операция интерпретируется в качестве фраз «тогда и только тогда», «необходимо и достаточно». Такая форма тоже очень часто используется в формулировке теорем.
· Штрих Шеффера определяет несовместимость высказываний. Эта операция ложна тогда и только тогда, когда оба операнда истинны Приведем таблицу истинности этой операции.

| 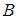
| 
|
Дата добавления: 2015-01-05; просмотров: 463; Мы поможем в написании вашей работы!; Нарушение авторских прав |