Энтропия. Ее статистический смысл.

Энтропия является мерой вероятности осуществления какого-либо макроскопического состояния. Количественная мера неупорядоченности. Это новая функция состояния, определяемая соотношением: dS=dq/T, где dq - поглощаемое системой тепло в обратимом равновесном процессе.В любом процессе приращение энтропии больше или равно приведенной теплоте процесса dq/T: dS ³ dq/T

Энтропия растет до максимального значения, соответствующего положению равновесия. Т.о., S дает критерий самопроизвольного протекания процесса (dS>0) и критерий равновесия (dS = 0, d2S < 0).

В рамках статистической физики мерой неупорядоченности системы, состоящей из большого числа частиц, является число возможных микросостояний, соответствующих данному макросостоянию (термодинамическая вероятность системы W). Микросостояние задается набором координат и импульсов всех частиц системы, а макросостояние - набором функций состояния (Т,Р.V,U и др). Число микросостояний очень велико, и термодинамическая вероятность >>1. Энтропия в статистической физике определяется по Больцману:

S=klnW, где к - постоянная Больцмана.

48. Изменение энтропии при квазиравновесных процессах(изобарный, изотермический, изохорный, адиабатический процессы если что))

Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:

изохорический: 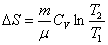, т.к. 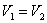; изобарический: т.к. Р1 = Р2;

изотермический: т.к. ; адиабатический: , т.к.

Отметим, что в последнем случае адиабатический процесс называют изоэнтропийным процессом, т.к. .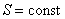
т.е. энтропия адиабатически изолированной системы может только возрастать (если есть необратимые процессы), или оставаться неизменной (если все процессы обратимые). – это закон возрастания энтропии.