
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Игровая модель рисков.
Особый раздел науки - теория игр позволяет хотя бы частично разрешать затруднения, возникающие при системном анализе в условиях противодействия. Интересно отметить, что одна из первых монографий по этим вопросам называлась "Теория игр и экономического поведения" и послужила своеобразным катализатором развития методов линейного программирования и теории статистических решений.
В качестве простого примера использования методов теории игр в экономике рассмотрим следующую задачу.
Пусть вы имеете всего три варианта стратегий в условиях конкуренции S1,S2 и S3 (например - выпускать в течение месяца один из 3 видов продукции). При этом ваш конкурент имеет всего два варианта стратегий C1 и C2 (выпускать один из 2 видов своей продукции, в каком то смысле заменяющей продукцию вашей фирмы). При этом менять вид продукции в течение месяца невозможно ни вам, ни вашему конкуренту.
Пусть и вам, и вашему конкуренту достоверно известны последствия каждого из собственных вариантов поведения, описываемые следующей таблицей.
Таблица 3.6
| C1 | C2 | |
| S1 | -2000 | + 2000 |
| S2 | -1000 | +3000 |
| S3 | +1000 | +2000 |
Цифры в таблице означают следующее:
· вы несете убытки в 2000 у.е., а конкурент имеет ту же сумму прибыли, если вы приняли стратегию S1, а конкурент применил C1;
· вы имеете прибыль в 2000 у.е., а конкурент теряет ту же сумму, если вы приняли S1 против C2;
· вы несете убытки в сумме 1000 у.е., а конкурент получает такую прибыль, если ваш вариант S2 оказался против его варианта C1 , и так далее.
Предполагается, что обе стороны имеют профессиональную подготовку в области ТССА и действуют разумно, соблюдая правила - вариант поведения принимают один раз на весь месяц, не зная, конечно, что предпринял на этот же месяц конкурент.
По сути дела, в чисто житейском смысле - это обычная "азартная" игра, в которой существует конечный результат, цель игры - выигрыш.
Этой цели добивается каждый игрок, но не каждый может ее добиться. Варианты поведения игроков можно считать ходами, а множество ходов - рассматривать как партию.
Пусть партия состоит всего лишь из одного хода с каждой стороны. Попробуем найти этот наилучший ход сначала для вашего конкурента - порассуждаем за него.
Так как таблица известна как вам, так и конкуренту, то его рассуждения можно промоделировать.
Вашему конкуренту вариант C2 явно невыгоден - при любом вашем ходе вы будете в выигрыше, а конкурент в проигрыше. Следовательно, со стороны вашего противника будет, скорее всего, принят вариант C1, доставляющий ему минимум потерь.
Теперь можно порассуждать за себя. Вроде бы вариант S2 принесет нам максимальный выигрыш в 3000 у.е., но это при условии выбора C2 вашим конкурентом, а он, скорее всего, выберет C1.
Значит наилучшее, что мы можем предпринять - выбрать вариант S3, рассчитывая на наименьший из возможных выигрышей - в 1000 у.е..
Ознакомимся с рядом общепринятых терминов теории игр:
· поскольку в таблице игры наш возможный выигрыш всегда равен проигрышу конкурента и наоборот, то эту специфику отображают обычно в названии - игра с нулевой суммой;
· варианты поведения игроков-конкурентов называют чистыми стратегиями игры, учитывая независимость их от поведения конкурента;
· наилучшие стратегии для каждого из игроков называют решением игры;
· результат игры, на который рассчитывают оба игрока (1000 у.е. прибыли для вас или столько же в виде проигрыша для конкурента) называют ценой игры; она в игре с нулевой суммой однакова для обеих сторон;
· таблицу выигрышей (проигрышей) называют матрицей игры, в данном случае - прямоугольной.
Рассмотренный выше ход рассуждений по поиску наилучшего плана игры в условиях конкуренции - не единственный способ решения задач. Очень часто намного короче и, главное, более логически стройным оказывается другой принцип поиска оптимальных игровых стратегий - принцип минимакса.
Для иллюстрации этого метода рассмотрим предыдущий пример игры с несколько видоизмененной матрицей.
Таблица 3.7
| C1 | C2 | |
| S1 | -2000 | - 4000 |
| S2 | -1000 | +3000 |
| S3 | +1000 | +2000 |
Повторим метод рассуждений, использованный для предыдущего примера.
· Мы никогда не выберем стратегию S1, поскольку она при любом ответе конкурента принесет нам значительные убытки.
· Из двух оставшихся разумнее выбрать S3, так как при любом ответе конкурента мы получим прибыль.
· Выбираем в качестве оптимальной стратегии S3.
Рассуждения нашего конкурента окажутся примерно такими же по смыслу. Понимая, что мы никогда не примем S1 и выберем, в конце концов, S3, он примет решение считать оптимальной для себя стратегию C1 - в этом случае он будет иметь наименьшие убытки.
Можно применить и иной метод рассуждений, дающий, в конце концов, тот же результат. При выборе наилучшего плана игры для нас можно рассуждать так:
· при стратегии S1 минимальный (min) "выигрыш" составит - 4000 у.е.;
· при стратегии S2 минимальный (min) "выигрыш" составит - 1000 у.е.;
· при стратегии S3 минимальный (min) выигрыш составит + 1000 у.е..
Выходит, что наибольший (max) из наименьших (min) выигрышей - это 1000 у.е. и сам бог велел полагать стратегию S3 оптимальной, с надеждой на ответный ход конкурента его стратегией C1. Такую стратегию и называют стратегией MaxiMin.
Если теперь попробовать смоделировать поведение конкурента, то для него:
· при стратегии C1 максимальный (max) проигрыш составит 1000 у.е.;
· при стратегии C2 максимальный (max) проигрыш составит 2000 у.е..
Значит, наш конкурент, если он будет рассуждать здраво, выберет стратегию C1, поскольку именно она обеспечивает наименьший (min) из наибольших (max) проигрышей. Такую стратегию и называют стратегией MiniMax.
Легко заметить, что это одно и то же - вы делаете ход S3 в расчете на ответ C1, а ваш конкурент - ход C1 в расчете на S3.
Поэтому такие стратегии называют минимаксными - мы надеемся на минимум максимальных убытков или, что одно и то же, на максимум минимальной прибыли.
В двух рассмотренных примерах оптимальные стратегии "противников" совпадали, принято говорить - они соответствовали седловой точке матрицы игры.
Метод минимакса отличается от стандартного пути логических рассуждений таким важным показателем как алгоритмичность. В самом деле, можно доказать, что если седловая точка существует, то она находится на пересечении некоторой строки S и некоторого столбца C. Если число в этой точке самое большое для данной строки и, одновременно, самое малое в данном столбце, то это и есть седловая точка.
Конечно, далеко не все игры обладают седловой точкой, но если она есть, то поиск ее при числе строк и столбцов в несколько десятков (а то и сотен) по стандартному логическому плану - дело практически безнадежное без использования компьютерных технологий.
Но, даже при использовании компьютера, писать программу для реализации всех возможных If ... Then придется на специальных языках программирования (например - язык Prolog). Эти языки великолепны для решения логических задач, но практически непригодны для обычных вычислений. Если же использовать метод минимакса, то весь алгоритм поиска седловой точки займет на языке Pascal или C++ не более 5...10 строк программы.
Рассмотрим еще один простой пример игры, но уже без седловой точки.
Таблица 3.8
| C1 | C2 | |
| S1 | -3000 | +7000 |
| S2 | +6000 | +1000 |
Задача в этом случае для нас (и для нашего разумного конкурента) будет заключаться в смене стратегий, в надежде найти такую их комбинацию, при которой математическое ожидание выигрыша или средний выигрыш за некоторое число ходов будет максимальным.
Пусть мы приняли решение половину ходов в игре делать с использованием S1, а другую половину - с S2. Конечно, мы не можем знать, какую из своих двух стратегий будет применять конкурент, и поэтому придется рассматривать два крайних случая его поведения.
Если наш конкурент все время будет применять C1, то для нас выигрыш составит 0.5·(-3000)+0.5·(+6000) = 1500 у.е..
Если же он все время будет применять C2, то на выигрыш составит 0.5·(+7000)+0.5·(+1000) = 4000 у.е..
Ну, это уже повод для размышлений, для анализа. В конце концов, можно прикинуть, а что мы будем иметь в случае применения конкурентом также смешанной стратегии? Ответ уже готов - мы будем иметь выигрыш не менее 1500 у.е., поскольку выполненные выше расчеты охватили все варианты смешанных стратегий конкурента.
Поставим вопрос в более общем виде - а существует ли наилучшая смешанная стратегия (комбинация S1 и S2) для нас в условиях применения смешанных стратегий (комбинации C1 и C2) со стороны конкурента? Математическая теория игр позволяет ответить на этот вопрос утвердительно - оптимальная смешанная стратегия всегда существует, но она может гарантировать минимум математического ожидания выигрыша. Методы поиска таких стратегий хорошо разработаны и отражены в литературе.
Таким образом, мы снова оказались в роли ЛПР - системный подход не может дать рецепта для безусловного получения выигрыша.
Нам и только нам, решать - воспользоваться ли рекомендацией и применить оптимальную стратегию игры, но при этом считаться с риском возможного проигрыша (выигрыш окажется гарантированным лишь при очень большом числе ходов).
Завершим рассмотрение последнего примера демонстрацией поиска наилучшей смешанной стратегии.
Пусть мы применяем стратегию S1 с частотой 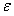 , а стратегию S2 с частотой
, а стратегию S2 с частотой 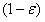 .
.
Тогда мы будем иметь выигрыш

при применении конкурентом стратегии C1
или будем иметь выигрыш

при применении конкурентом стратегии C2.
Теория игр позволяет найти наилучшую стратегию для нас из условия
W(C1) = W(C2); {3 - 16}
что приводит к наилучшему значению 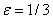 и математическому ожиданию выигрыша величиной в (-3000)·(1/3)+(+6000)·(2/3)=3000 у.е..
и математическому ожиданию выигрыша величиной в (-3000)·(1/3)+(+6000)·(2/3)=3000 у.е..
Дата добавления: 2015-01-16; просмотров: 244; Мы поможем в написании вашей работы!; Нарушение авторских прав |