Линейное программирование.

В качестве примера практического использования приведенного выше математического аппарата рассмотрим процедуру выбора продуктов питания, которая может быть использована для определения так называемой потребительской корзины.

Пусть имеется n продуктов (хлеб, мясо, молоко, картофель и т.д.) и m полезных веществ (жиры, белки, углеводы и т.п.), необходимых для жизнедеятельности человека. Обозначим через аij — содержание j-го вещества в единице i-го продукта, через b_j — потребность индивидуума в j-м веществе (скажем, в месяц) и через c_i — цену единицы i-го продукта.

Обозначив потребление индивидуумом i-го продукта через хi, получаем задачу о выборе наиболее дешевого рациона питания (стоимости месячной продовольственной потребительской корзины) [11]:

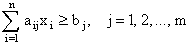
при ограничениях

Поскольку и целевая функция, и ограничения линейны, то данная задача называется задачей линейного программирования, в отличие от более распространенных задач нелинейного программирования, в которых имеет место нелинейность целевой функции и (или) ограничений.

Выясним, что представляет собой допустимая область на плоскости х₁0х₂ в случае только двух продуктов x₁ и x₂. Из неравенств (2.2) вытекает, что ДО расположена в первом квадранте, а каждое неравенство (2.1) геометрически определяет множество точек, лежащих по одну сторону от прямой (рис. 14). Следовательно, для трех полезных веществ (m=3) ДО представляет собой неограниченное множество (рис. 15).

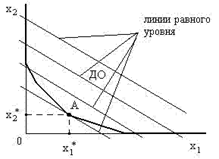
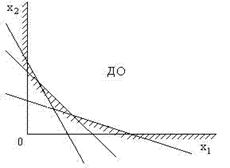
Рис. 14. Допустимая область при одном ограничении

Рис. 15. Допустимая область при трех ограничениях

Рис. 16. Геометрическая интерпретация задачи

Введем линии равного уровня целевой функции, т.е. линии, на которых в плоскости х₁0х₂ целевая функция

принимает постоянное значение. Очевидно, каждая такая линия является прямой.

Для графического нахождения оптимального решения следует наносить линии уровня до тех пор, пока хотя бы одна точка какой-то линии будет находиться в ДО. При этом эта линия коснется либо какой-то вершины, либо какого-то ребра допустимой области (в нашем случае это точка А) (рис. 16).

На практике для решения задач линейного программирования используется так называемый симплекс-метод.

Градиентный метод

Пусть имеется целевая функцию f(X). Надо найти ее экстремум.

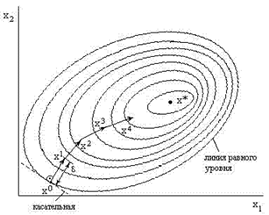
Выбирается некоторая точка Х⁰ — стартовая точка. В ней определяется grad, если решается задача максимизации, и анти-grad, если решается задача минимизации. Вдоль этого вектора делается шаг e, который завершается в точке Х¹. В этой точке вновь определяется grad, снова делается шаг e и т.д.

Критерием остановки вычислительного процесса является значение grad, равное нулю.

Рис. 17. Поиск экстремума функции f(X)

Данный метод имеет следующие недостатки:

1) при большом шаге можно проскочить экстремум;

2) при малом шаге увеличивается время расчета;

3) данный метод плохо работает в случае оврагообразных целевых функций;

4) метод плохо работает в задачах условной оптимизации: grad упирается в какое-нибудь ограничение и дальше процесс поиска экстремума прекращается;

5) при многоэкстремальной целевой функции результатом может оказаться локальный экстремум;

6) имеются трудности с выработкой критерия останова вычислительного процесса.

Метод сканирования (перебора)

Среди методов принятия решения перебор вариантов (метод проб и ошибок) занимает особое место. С древних времен он широко использовался для решения подобных задач.

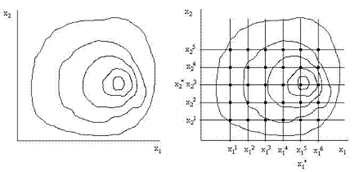
Пусть требуется минимизировать функцию двух переменных f(Х) = f(x₁, x₂). На рис. 18, а приведены линии равного уровня этой функции.

Допустим, что переменная х₁ принимает 6 значений: х₁= х₁¹, х₁², …, х₁⁶, а переменная х_{2 – 5} значений: х₂= х₂¹, х₂², …, х₂⁵.

a) б)Рис. 18. Поиск экстремума методом сканирования

Суть метода заключается в определении и сравнении значений целевой функции во всех узлах сетки (рис. 18 б). Расчет обычно начинается с левого нижнего узла или слева направо, или снизу вверх, в зависимости от того, какая переменная меняется во внутреннем цикле. Алгоритм метода сканирования для данного случая в виде блок-схемы приведен на рис. 19.

Рис. 20. Иллюстрация неправильной настройки метода сканирования

Критерием остановки процесса является реализация всех вычислений, число которых определяется по формуле:

N = n₁*n₂* … *nn , где n_i — число значений, принимаемых i-й переменной.

Недостатки этого метода:

1) невысокая точность (она определяется половиной шага); из рис. 18 б видно, что точка (х₁*, х₂*), принятая за искомую, имеет координаты (х₁⁵, х₂³), хотя понятно, что истинный экстремум находится в окрестности этой точки;

2) с уменьшением шага возрастает время расчета и даже на быстродействующем компьютере оно может составить десятки минут и даже часов; особенно это заметно при большом числе переменных (n > 8¸10);

3) при неудачном выборе диапазонов изменения переменных можно получить неправильный результат (рис. 20);

4) в случае сложной конфигурации ДО много расчетов будет выполняться "вхолостую", т.е. целевая функция будет рассчитываться в точках, находящихся за пределами ДО.

Достоинства

1) простота, наглядность;

2) для многоэкстремальных целевых функций имеется возможность найти глобальный экстремум.

Метод сканирования на практике эффективен, когда число переменных не превышает 5/8, в противном случае даже на современных персональных компьютерах затраты времени на поиск результата могут быть очень значительными.

Метод Гаусса-Зейделя (покоординатного спуска)

Пусть требуется оптимизировать функцию f(Х) = f(x₁, x₂, …, x_n).

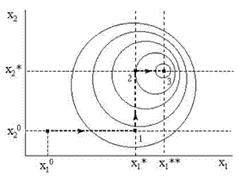Выбирается некоторая стартовая точка Х₀ (рис. 21). Из нее начинается процесс поиска, при этом меняется только одна переменная, например, х₁. При изменении данной переменной оптимум целевой функции находится одним из известных методов: градиента, сканирования и т.д. Получается точка с координатами х₁*, х₂0, …, х_n0. После этого, из найденной точки организуется новый цикл, при этом меняется переменная х2. Получают точку х₁*, х₂*, х₃0, …, х_n0 и т.д. до изменения хn. После этого организуется новый цикл по переменной х₁ и получается точка х₁**, х₂*, …, х_n*. Критерием остановки процесса является незначительное изменение значений как переменных, так и целевой функции.

Рис. 21. Поиск экстремума методом Гаусса-Зейделя

Из рис. 21 видно, что для нахождения результата потребовалось всего три цикла:

• в первом – получена точка 1 с координатами (х₁*, х₂0) (на рисунке подобные точки располагаются или примерно в середине интервала между одной линией уровня, или в месте касания следующей линии уровня);

• во втором цикле получена точка 2 с координатами (х₁, х₂*);

• в третьем цикле получена точка 3 с координатами (х₁**, х₂*); эта точка практически совпадает, как видно из рисунка, с действительным экстремумом целевой функции.

Недостатки метода:

1) метод малоэффективен, когда главные оси линий уровня не параллельны осям координат;

2) метод плохо работает при наличии ограничений;

3) в качестве результата может быть получен локальный экстремум;

4) возникают трудности с выработкой критерия останова вычислительного процесса.

Метод случайного поиска (Монте-Карло)

Рассмотрим суть метода на следующем простом примере.

Пусть требуется определить площадь сложной фигуры, расположенной в квадрате площадью S. Выберем в площади квадрата N случайных точек с равномерным законом распределения. Обозначим через N' число точек, попавших в площадь фигуры (рис. 22).

Рис. 22. Определение площади фигуры

Тогда искомую площадь можно приближенно определить по формуле:

При N стремиться к бесконечности рассчитанная площадь будет стремиться к действительной.

На этом принципе строится работа случайного поиска. Предположим, требуется найти экстремум функции двух переменных f(Х)=f(x₁, x₂). Для каждой переменной назначается интервал изменения, в котором она выбирается случайным образом. В точке Х' определяется значение целевой функции, которое запоминается. Случайно выбирается новое значение Х" и f(X") сравнивается с f(Х'). Если функция в новой точке Х'' имеет лучшее значение, то запоминается Х'' и f(X''). Затем выбирается Х''' и т.д.

Можно доказать, что когда число случайных испытаний N стремиться к бесконечности, то точка с наилучшим значением целевой функции будет соответствовать глобальному экстремуму.

Обычно координаты случайных точек определяются с помощью программного датчика случайных чисел. В простейшем случае распределение вероятностей для каждой переменной принимается равномерным.

Критерием остановки процесса является выработка заданного количества случайных точек.

Достоинства метода:

1) простота и наглядность;

2) универсальность;

3) некритичность к размерности задачи: с ростом числа переменных время расчета растет существенно медленнее, чем в методе сканирования.

Недостатки:

1) в ряде случаев (особенно при малых N) недостаточная точность;

2) для задач условной оптимизации большое число случайных испытаний происходит вхолостую (за пределами ДО), что непроизводительно увеличивает время расчета.