Основные базовые модели диверсификации рисков

Диверсификация — общепринятое средство сокращения многих видов риска. С увеличением числа элементов набора (портфеля) уменьшается общий размер риска. Однако только в случае, когда риск может быть измерен и представлен в виде статистического показателя, управление риском получает надежное основание, а последствия диверсификации поддаются анализу с привлечением методов математической статистики.

В инвестиционном анализе и страховом деле риск часто измеряется с помощью таких стандартных статистических характеристик, как дисперсия и среднее квадратическое (стандартное) отклонение. Обе характеристики измеряют колебания дохода от инвестиций. Чем они больше, тем выше рассеяние показателей дохода вокруг средней и, следовательно, значительнее степень риска.

Напомним, что между дисперсией Dи средним квадратическим отклонением σ существует следующее соотношение:

В свою очередь, выборочная дисперсия относительно средней находится как

где n — количество наблюдений;

х — средняя случайной переменной х.

Как известно, среднее квадратическое отклонение имеет то неоспоримое достоинство, что при близости реального распределения (речь здесь идет о распределении дохода от инвестиций) к нормальному, что, строго говоря, должно быть статистически проверено, этот параметр может быть использован для

определения границ, в которых с заданной вероятностью следует ожидать значение случайной переменной. Так, например, с вероятностью 68% можно утверждать, что значение случайной переменной х (в нашем случае доход) находится в границах ~х±σ , а с вероятностью 95% — в пределах х±2σ и т. д. (рис. 4.1).

Диверсификация инвестиций и дисперсия дохода

Определим теперь, что дает диверсификация для уменьшения риска, и выявим условия, когда эта цель достигается. В качестве объекта анализа примем некоторый абстрактный портфель ценных бумаг (далее для краткости — портфель). Такой выбор объясняется методологическими преимуществами — в этом случае проще выявить зависимости между основными переменными. Однако многие из полученных результатов без большой натяжки можно распространить и на производственные инвестиции.

В § 4.1 отмечалось, что в качестве измерителя риска в долгосрочных финансовых операциях широко распространена такая мера, как дисперсия дохода во времени. Диверсификация портфеля при правильном ее применении приводит к уменьшению этой дисперсии при всех прочих равных условиях. Диверсификация базируется на простой гипотезе. Если каждая компонента портфеля (в рассматриваемой задаче — вид ценной бумаги) характеризуется некоторой дисперсией дохода, то доход от портфеля имеет дисперсию, определяемую его составом. Таким образом, изменяя состав портфеля, можно менять суммарную дисперсию дохода, а в некоторых случаях свести ее к минимуму.

Итак, пусть имеется портфель из n видов ценных бумаг. Доход от одной бумаги вида iсоставляет величину d,.Суммарный доход А равен:

где а, — количество бумаг вида i.

Если d_tпредставляет собой средний доход от бумаги вида ;', то величина А характеризует средний доход от портфеля бумаг в целом.

Для начала положим, что показатели доходов различных видов бумаг являются статистически независимыми величинами (иначе говоря, не коррелируют между собой). Дисперсия дохода портфеля (обозначим ее D)в этом случае находится как

где D_i— дисперсия дохода от бумаги вида i.

Для упрощения, которое нисколько не повлияет на результаты дальнейших рассуждений, перейдем от абсолютного измерения количества ценных бумаг к относительному. Пусть теперь а_i характеризует долю в портфеле бумаги вида i. Соответственно 0 < а_i < 1; ∑ а_i =1.

Для зависимых в статистическом смысле показателей дохода отдельных бумаг дисперсию суммарного дохода находим следующим образом':

¹Доказательства справедливости формул (4.2) и (4.3) можно найти в пособиях по математической статистике.

где D_i — дисперсия дохода от бумаги вида i;

r_ij —коэффициент корреляции дохода от бумаг вида i и j;

σ_iи σ_j —среднее квадратическое отклонение дохода у бумаг вида i и j.

Коэффициент корреляции двух случайных переменных х и у¹, как известно, определяется по формуле:

где х, у — средние (в нашем случае средние доходы двух видов бумаг).

Для расчетов часто применяется следующая рабочая формула:

Поскольку коэффициент корреляции может быть как положительной, так и отрицательной величиной, то при положительной корреляции дисперсия суммарного дохода увеличивается, при отрицательной — сокращается. В самом деле, при заметной отрицательной корреляции положительные отклонения от среднего дохода одних бумаг погашаются отрицательными отклонениями у других. И наоборот, при положительной корреляции отклонения суммируются, что увеличивает общую дисперсию и риск.

Напомним следующие свойства коэффициента корреляции:

• коэффициент не имеет размерности, следовательно, он сопоставим для разных рядов данных;

• величина r_xy лежит в пределах от -1 до +1. Значение r=+1 говорит о том, что между переменными существует полная положительная корреляция, т. е. наблюдается функциональная линейная зависимость — с увеличением x линейно растет у. При r=-1 наблюдается отрицательная линейная зависимость.

Проследим теперь, каково влияние масштаба диверсификации на размер риска. Под масштабом диверсификации будем понимать количество объектов, возможных для инвестирования (количество видов ценных бумаг). Обратимся к условному примеру, который позволяет наиболее отчетливо выделить влияние указанного фактора.

Итак, пусть портфель состоит из бумаг различного вида, но имеющих одинаковую дисперсию дохода σ²₀. Удельные веса в портфеле каждого вида бумаг также одинаковы, а общая сумма вложений равна 1. Положим, что показатели доходности у отдельных видов бумаг статистически независимы, т. е. применима формула (4.2). В этих условиях для оценки величины среднего квадратического отклонения дохода портфеля получим:

где n — количество видов ценных бумаг.

Воспользуемся приведенной формулой и определим дисперсию дохода для портфеля, состоящего из двух и трех видов бумаг. Так, для двух бумаг имеем

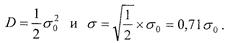
Для трех видов бумаг квадратическое отклонение портфеля составит 0,58σ₀. Таким образом, с увеличением числа составляющих портфеля риск уменьшается даже при одинаковой дисперсии составляющих элементов, однако действенность диверсификации снижается. Соответствующая зависимость изображена на рис. 4.2.

Увеличение масштабов диверсификации оказывает наибольшее влияние на начальных стадиях — при малых значениях п. Например, в рамках рассмотренного примера переход от одного вида бумаг к четырем сокращает квадратическое отклонение на 50%, а от одного к восьми — на 65%.

Полученные выше выводы в отношении тенденции изменения среднего квадратического отклонения в зависимости от числа составляющих при условии, когда дисперсии составляющих одинаковы, справедливы и для более общих случаев. Однако зависимость этого параметра от степени диверсификации проявляется здесь не столь четко.

Посмотрим теперь, как изменяются доход и величина риска при изменении структуры портфеля. Для этого вернемся к формулам (4.2) и (4.3) и запишем их только для двух видов бумаг (X и Y).Такой анализ вряд ли имеет практическое значение. Однако с его помощью наглядно демонстрируются последствия "смешения" ценных бумаг с различными доходностью и дисперсией. Для независимых доходов получим:

и для зависимых доходов

Причем а_y= 1 - а_x.

В этом случае среднее значение суммарного дохода определяется как

Положим, что d_y>d_x. и Увеличение масштабов диверсификации оказывает наибольшее влияние на начальных стадиях — при малых значениях п. Например, в рамках рассмотренного примера переход от одного вида бумаг к четырем сокращает квадратическое отклонение на 50%, а от одного к восьми — на 65%.

Полученные выше выводы в отношении тенденции изменения среднего квадратического отклонения в зависимости от числа составляющих при условии, когда дисперсии составляющих одинаковы, справедливы и для более общих случаев. Однако зависимость этого параметра от степени диверсификации проявляется здесь не столь четко.

Посмотрим теперь, как изменяются доход и величина риска при изменении структуры портфеля. Для этого вернемся к формулам (4.2) и (4.3) и запишем их только для двух видов бумаг (X и Y).Такой анализ вряд ли имеет практическое значение. Однако с его помощью наглядно демонстрируются последствия "смешения" ценных бумаг с различными доходностью и дисперсией. Для независимых доходов получим: σ_y > σ_x. Тогда увеличение доли бумаг второго вида увеличивает доходность портфеля.

Так, на основе (4.7) получим

Что касается дисперсии, то, как следует из (4.6), положение не столь однозначно и зависит от знака и степени корреляции. В связи с этим подробно рассмотрим три Что касается дисперсии, то, как следует из (4.6), положение не столь однозначно и зависит от знака и степени корреляции.

В связи с этим подробно рассмотрим три ситуации:

1. полная положительная корреляция доходов (r_xy= +1) ,

2. полная отрицательная корреляция (r_xy= -1),

3. независимость доходов или нулевая корреляция (r_xy = 0).

В первом случае увеличение дохода за счет включения в портфель бумаги вида Yпомимо Х сопровождается ростом как дохода, так и дисперсии.

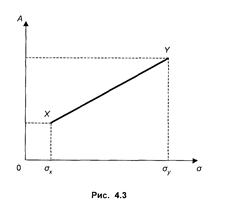
Для портфеля, содержащего оба вида бумаг, квадратическое отклонение находится в пределах σ_x < σ <σ_y (рис. 4.3).

Для частного случая, когда σ_x = σ_y = σ, получим по формуле (4.6) D =σ². Иначе говоря, "смешение" инвестиций здесь не окажет никакого влияния на величину дисперсии.

При полной отрицательной корреляции доходов динамика квадратического отклонения доходов от портфеля более сложная.

По мере движения от точки Х к точке У эта величина сначала сокращается и доходит до нуля в точке В, затем растет (рис. 4.4).

В последней из рассматриваемых ситуаций (r_xy= 0) квадратическое отклонение при увеличении доли бумаги Y проходит точку минимума, равного σ_m, далее оно растет до σ_y(рис. 4.5).

Совместим теперь все три графика на одном (рис. 4.6). Как видим, все возможные варианты зависимости "доход — среднее квадратическое отклонение" находятся в треугольнике XBY.

Из сказанного непосредственно следует, что эффективность диверсификации (в отношении сокращения риска) наблюдается только при отрицательной или, в крайнем случае, нулевой корреляции.

Пример 1

Портфель должен состоять из двух видов бумаг, параметры которых:

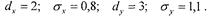
Доход от портфеля: А = 2а_x + 3a_y.Таким образом, доход в зависимости от величины долей находится в пределах 2 < А < 3 . Дисперсия суммы дохода составит:

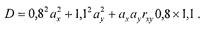
Определим доход и дисперсию для портфеля с долями, равными, допустим, 0,3 и 0,7. Получим по формулам (4.5) и (4.6):

Таким образом, при полной положительной корреляции D= 0,854, при полной отрицательной корреляции D=0,484. В итоге с вероятностью 95% можно утверждать, что суммарный доход находится в первом случае в пределах

во втором он определяется пределами

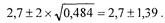
При нулевой корреляции доходов пределы составят

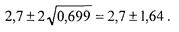
Продолжим анализ с двумя бумагами и проследим, как влияет включение в портфель безрисковой (risk free)инвестиции'.

Для этого заменим в портфеле бумагу Yс параметрами

на бумагу с такой же доходностью, но с нулевой дисперсией. Доходность портфеля от такой замены, разумеется, не изменится. Что же касается дисперсии, то она теперь составит:

Дисперсия и среднее квадратическое отклонение дохода портфеля теперь зависят от удельного веса безрисковой составляющей:

Таким образом, "разбавление" портфеля безрисковой бумагой снижает риск портфеля в целом, а квадратическое отклонение дохода портфеля определяется убывающей линейной функцией доли безрисковой бумаги. Если d_x > d_y(в противном случае проблема выбора портфеля отпадает — он должен состоять только из безрисковых бумаг), то доход от портфеля по мере увеличения доли безрисковой бумаги уменьшается от d_xдо d_y а величина квадратического отклонения сокращается от σ_x до 0 (рис. 4.7). И наоборот, рост доли рисковой бумаги увеличивает как риск, так и доход.

Последнее утверждение для портфеля, состоящего из двух видов бумаг, иллюстрируется уравнением (4.10):

¹В странах со стабильной экономикой безрисковой обычно считается ценная бумага, выпущенная государственным казначейством.

В свою очередь, на основе (4.9) находим

В итоге получим интересное соотношение

Дробь в приведенном выражении иногда называют рыночной ценой риска. Если эта величина равна, скажем, 0,5, то при росте квадратического отклонения на 1% доход увеличится на 0,5%.