
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Магнитное поле и его характеристики. Закон полного тока. Магнитное поле проводника с током
При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34). Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с.
При анализе магнитных полей важное значение имеет закон полного тока, который в интегральной форме имеет вид:

(3.3)
и гласит о том, что линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.
Под полным током понимают алгебраическую сумму токов проводимости, переноса и смещения.
В дифференциальной форме закон полного тока можно записать следующим образом:

Магнитное поле проводника с током.При прохождении тока по прямолинейному проводнику вокруг него возникает магнитное поле (рис. 38). Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.
Направление магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику. Направление магнитных силовых линий можно определить по правилу буравчика. Его формулируют следующим образом. Если поступательное движение буравчика 1 (рис. 39, а) совместить с направлением тока 2 в проводнике 3, то вращение его рукоятки укажет направление силовых линий 4 магнитного поля вокруг проводника. Например, если ток проходит по проводнику в направлении от нас за плоскость листа книги (рис. 39, б), то магнитное поле, возникающее вокруг этого проводника, направлено по часовой стрелке. Если ток по проводнику проходит по направлению от плоскости листа книги к нам, то магнитное поле вокруг проводника направлено против часовой стрелки. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле. При изменении направления тока магнитное поле также изменяет свое направление.
По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля и его напряженность уменьшаются. Напряженность магнитного поля в пространстве, окружающем проводник,
31) Законы Кирхгоффа и Ома для магнитной цепи (формулировка, математическая запись, физический смысл).
| Наименование закона | Аналитическое выражение закона | Формулировка закона |
| Первый закон Кирхгофа | 
| Алгебраическая сумма магнитных потоков в узле магнитопровода равна нулю. |
| Второй закон Кирхгофа | 
| Алгебраическая сумма падения магнитного напряжения вдоль замкнутого контура равна алгебраической сумме МДС, действующих в контуре. |
| Закон Ома |  , где , где 
| Падение магнитного напряжения на участке магнитопровода длинной 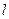 равно произведению магнитного потока и магнитного сопротивления равно произведению магнитного потока и магнитного сопротивления  участка. участка.
|
Сформулированные законы и понятия магнитных цепей позволяют провести формальную аналогию между основными величинами и законами, соответствующими электрическим и магнитным цепям, которую иллюстрирует табл. 4.9.
Аналогия величин и законов для электрических и магнитных цепей
Таблица 4.9.
| Электрическая цепь | Магнитная цепь |
 , А – ток , А – ток
|  , Вб – поток , Вб – поток
|
 , В – ЭДС , В – ЭДС
|  , А – МДС , А – МДС
|
 , Ом – электрическое сопротивление , Ом – электрическое сопротивление
|  , ,  – магнитное сопротивление – магнитное сопротивление
|
 , В – электрическое напряжение , В – электрическое напряжение
|  , А – магнитное напряжение , А – магнитное напряжение
|
 – первый закон Кирхгофа – первый закон Кирхгофа
|  – первый закон Кирхгофа – первый закон Кирхгофа
|
 – второй закон Кирхгофа – второй закон Кирхгофа
| 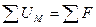 – второй закон Кирхгофа – второй закон Кирхгофа
|
 – закон Ома – закон Ома
|  – закон Ома – закон Ома
|
32) Закон электромагнитной индукции. Определение направления ЭДС самоиндукции.
Если по проводнику протекает переменный ток, то вокруг этого проводника он создает переменный магнитный поток, который создает переменное потокосцепление, а нон в свою очередь порождает ЭДС.
Таким образом, ЭДС каждой катушки определяется алгебраической суммой ЭДС самоиндукции и взаимной индукции. Для определения знака ЭДС взаимной индукции размечают зажимы индуктивно связанных элементов цепи. Два зажима называют одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции складываются. Такие выводы обозначают на схемах одинаковыми условными значками, например, точками или звездочками (рис. 2.20 а, б). Одинаково направленные токи  и
и  (рис. 2.20 а) относительно зажимов
(рис. 2.20 а) относительно зажимов  и
и  вызывают совпадающие по направлению потоки самоиндукции
вызывают совпадающие по направлению потоки самоиндукции  (
(  ) и взаимной индукции
) и взаимной индукции  (
(  ). Следовательно, зажимы
). Следовательно, зажимы  и
и  являются одноименными. Одноименной является и другая пара зажимов
являются одноименными. Одноименной является и другая пара зажимов  и
и  , но условными значками обозначают только одну пару одноименных выводов, например,
, но условными значками обозначают только одну пару одноименных выводов, например,  и
и  (рис. 2.20 а). Если токи
(рис. 2.20 а). Если токи  и
и  направлены неодинаково относительно одноименных зажимов (рис. 2.20 б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.
направлены неодинаково относительно одноименных зажимов (рис. 2.20 б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.
На схемах магнитопроводы, как правило, не показывают и ограничиваются только обозначением одноименных зажимов (рис. 2.20 в, г).
Одноименные зажимы можно определить опытным путем. Для этого одну из катушек включают в цепь источника постоянного тока, а к другой присоединяют вольтметр постоянного тока. Если в момент подключения источника стрелка измерительного прибора отклоняется, то зажимы индуктивно связанных

Рис. 2.20
катушек, подключенные к положительному полюсу источника и положительному зажиму измерительного прибора, являются одноименными.
Определим знаки ЭДС и напряжения взаимной индукции. Допустим, первая катушка (рис. 2.20 а) разомкнута, а во второй протекает ток  . Выберем положительные направления для
. Выберем положительные направления для  одинаковыми относительно одноименных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда
одинаковыми относительно одноименных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда  0, потенциал зажима b больше потенциала зажима а, следовательно,
0, потенциал зажима b больше потенциала зажима а, следовательно,  0.
0.
(adsbygoogle = window.adsbygoogle || []).push({});
По правилу Ленца знаки  и
и  всегда противоположны, поэтому
всегда противоположны, поэтому
 .
.
В комплексной форме уравнение имеет вид
 (2.50)
(2.50)
При встречном включении катушек (рис. 2.20 б)
 . (2.51)
. (2.51)
Из (2.50) и (2.51) видно, что вектор напряжения на взаимной индуктивности  сдвинут по фазе относительно вектора тока
сдвинут по фазе относительно вектора тока  на угол ±90°.
на угол ±90°.
Сопротивление  называется сопротивлением взаимной индуктивности, а
называется сопротивлением взаимной индуктивности, а  – комплексным сопротивлением взаимной индуктивности.
– комплексным сопротивлением взаимной индуктивности.
Таким образом, при согласном направлении токов падение напряжения на взаимной индуктивности имеет знак «плюс», при встречном – знак «минус».
33) ЭДС самоиндукции. Энергия магнитного поля. Магнитный поток и магнитное напряжение.
Самоиндукция. Энергия магнитного поля window.top.document.title = "1.21. Самоиндукция. Энергия магнитного поля";
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
|
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукциииндуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна или 1 Гн, если при силе постоянного тока 1. А собственный поток равен 1 Вб:
| 1 Гн = 1 Вб / 1 А. |
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой (см. § 1.17)
| B = μ0In, |
где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.
Магнитный поток, пронизывающий все N витков соленоида, равен
| Φ = B·S·N = μ0n2SlI. |
Следовательно, индуктивность соленоида равна
|
где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз (см. § 1.17); поэтому индуктивность катушки с сердечником также увеличивается в μ раз:
|
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна

|
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

|
| Рисунок 1.21.1. Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает. |
Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2RΔt.
Ток в цепи равен

|
Выражение для ΔQ можно записать в виде
| ΔQ = –LIΔI = –Φ(I)ΔI. |
В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I0 до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I0 до 0. Это дает

|
Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного на рис. 1.21.2 треугольника.

|
| Рисунок 1.21.2. Вычисление энергии магнитного поля. |
Таким образом, энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
|
Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить:

|
где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина
|
равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.
Определение магнитного потока:
Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.
Формула магнитного потока:
Ф = BS cos α
здесь α - угол между направлением вектора магнитной индукции B и нормалью к поверхности S.
Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её. А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 108 мкс. Соответственно 1 мкс = 10-8 вб.
Магнитный поток является скалярной величиной.
Магнитное напряжение на прямолинейном участке контура есть произведение длины участка и проекции вектора магнитной напряженности на этот прямолинейный участок. Всё это относится к однородному магнитному полю. Если поле не однородно или участок контура не прямой, то выбирают малую часть контура, которую можно считать прямолинейной, а магнитное поле в месте расположения этого участка однородным.
На картинке показано однородное магнитное поле с вектором напряженности H и криволинейный контур L. Контур криволинейный, поэтому определить магнитное напряжение сразу на всём контуре невозможно. Выделим на контуре отрезок ΔL (показан жирной линией), который можно считать прямолинейным, и будем находить магнитное напряжение только на этом участке. Проекция вектора напряженности магнитного поля H на направление отрезка ΔL равна:
HL = H * cos α
где α - угол между вектором H и отрезком ΔL.
Магнитное напряжение на отрезке ΔL (формула магнитного напряжения):
Um = (H * cos α) * ΔL = HL * ΔL
Выделив прямолинейные участки на остальных частях контура L, найдём магнитные напряжения на них. Тогда полное магнитное напряжение на всём контуре L будет равно сумме магнитных напряжений участков:
UL = Σ HL * ΔL
Измеряется магнитное напряжение в амперах: А.
Магнитное напряжение вдоль контура L зависит от формы этого контура.
Дата добавления: 2015-01-17; просмотров: 389; Мы поможем в написании вашей работы!; Нарушение авторских прав |