
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Начальная фаза. Сдвиг фаз
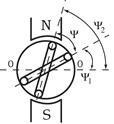
| Предположим, что в магнитном поле генератора находится два одинаковых витка, сдвинутых в пространстве друг относительно друга на угол 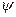 . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды. . При вращении в них буду находится ЭДС одинаковой частоты и амплитуды.
|
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени 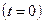 ЭДС витка будет:
ЭДС витка будет:
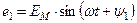
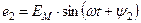
В этих выражениях углы  и
и 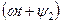 называются фазными, или фазой. Углы
называются фазными, или фазой. Углы 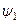 и
и 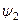 называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
называются начальной фазой. Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
(adsbygoogle = window.adsbygoogle || []).push({});
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
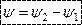
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
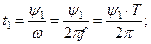
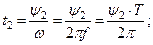
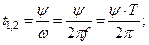

| Если угол сдвига фаз составляет 1800, то такие ЭДС находятся в противофазе |
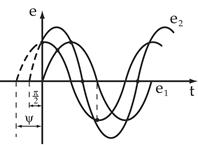
Графическое изображение синусоидальных величин
Синусоидальные величины можно изображать графически при помощи синусоид или вращающихся векторов.
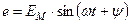
Любая синусоидальная величина характеризуется:
1. амплитудой;
2. угловой частотой;
3. начальной фазой.

При изображении величины с помощью синусоиды ординаты синусоиды в масштабе представляют собой мгновенное значение, абсциссы – промежутки времени.
При этом длина вектора равна амплитудному значению величины, угол  между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью
между положительным направлением оси абсцисс и векторов даст начальную фазу. Вектор вращается против часовой стрелки с угловой скоростью  . Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
. Проекция конца вектора на ось ординат даст мгновенное значение синусоидальной величины.
Совокупность нескольких синусоид называется синусоидальной (волновой) диаграммой.
Совокупность нескольких векторов называется векторной диаграммой.
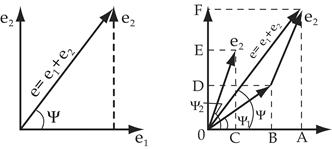
Сложение и вычитание синусоидальных величин

 .
.
Для сложения двух синусоидальных величин с помощью синусоид необходимо сложить их ординаты в каждый момент времени.
Для того, чтобы сложить две величины с помощью векторов, необходимо к концу первого вектора добавить второй, не изменяя его величины и направления. Соединив начало первого вектора с концом второго, получим суммарный вектор.
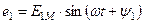


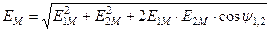
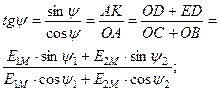
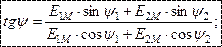
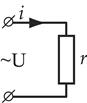
Цепи переменного тока с активным сопротивлением

| 
|
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.

| - постоянный ток |

| - переменный ток |
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом. Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.
| 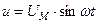 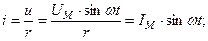 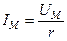 . .
|
Разделив обе части равенства на  , получим действующие значения
, получим действующие значения 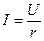 .
.
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.

| 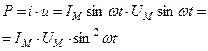 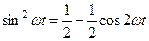 
|

Таким образом, мощность состоит из постоянной составляющей  и переменной составляющей
и переменной составляющей 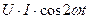 , среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности
, среднее значение которых за период равно нулю. Таким образом, постоянная составляющая мощности  выражает среднее за период значение мощности и называется активной мощностью:
выражает среднее за период значение мощности и называется активной мощностью:
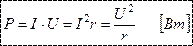
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением r только потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.


Цепи переменного тока с индуктивностью
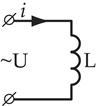
| Допустим, что под действием напряжения в этой цепи протекает ток. Под действием переменного тока в катушке возникает переменный магнитный поток, который наводи в ней ЭДС самоиндукции. 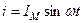
|
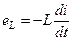
ЭДС самоиндукции  в любой момент времени уравновешивается напряжением:
в любой момент времени уравновешивается напряжением:
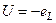

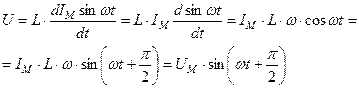

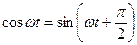

Т.о. в цепи с индуктивностью напряжение опережает ток на угол 900.
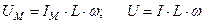
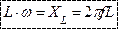
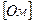 - индуктивное (реактивное) сопротивление.
- индуктивное (реактивное) сопротивление.
 - закон Ома для цепи с индуктивностью.
- закон Ома для цепи с индуктивностью.
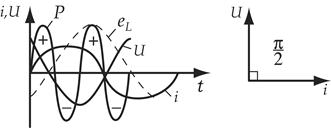
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
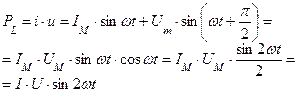
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
 - цепь работает потребителем
- цепь работает потребителем
 - цепь работает генератором.
- цепь работает генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:

Энергия, запасенная в магнитном поле катушки, равна
Цепь переменного тока с емкостью
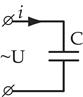
|  Под действием этого напряжения конденсатор будет разряжаться и заряжаться. Мгновенное значение заряда на обкладках конденсатора: Под действием этого напряжения конденсатор будет разряжаться и заряжаться. Мгновенное значение заряда на обкладках конденсатора: 
|


 - закон Ома для цепи с емкостью.
- закон Ома для цепи с емкостью.
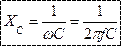 - реактивное емкостное сопротивление
- реактивное емкостное сопротивление
Т.о. ток в цепи с емкостью опережает напряжение на угол 900.
Физически емкостное сопротивление характеризует препятствие, оказываемое переменному току цепью с емкостью. В результате поляризации диэлектрика конденсатора в нем образуется свое внутренне электрическое поле, которое направлено противоположно внешнему полю, приложенному к диэлектрику.
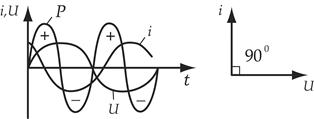
Мощность цепи:
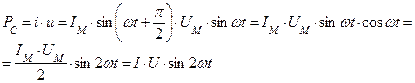
Мощность изменяется с двойной частотой относительно тока и напряжения. В течении первой четверти периода, когда напряжение, приложенное к конденсатору, возрастает, мгновенная мощность положительна. Это означает, что конденсатор получает и запасает энергию источника в виде электрического поля.
В течении второй четверти, когда напряжение, приложенное к конденсатору, уменьшается, запасенная энергия возвращается к источнику, т.е.
 - цепь работает потребителем;
- цепь работает потребителем;
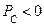 - цепь работает источником.
- цепь работает источником.
Максимальное значение мощности цепи с емкостью называют реактивной емкостной мощностью:
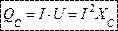
Она характеризует скорость обмена энергией между источником и цепью с емкостью.
Максимальное значение энергии, запасенной в цепи:

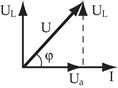
Неразветвленная цепь переменного тока с активным сопротивлением и индуктивностью
Таким сопротивлением (активным и индуктивным) обладают катушки индуктивности, обмотки трансформаторов и электрических машин.
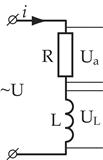
| 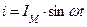  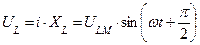 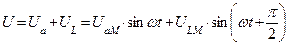 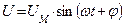
|
Т.о. напряжение опережает ток в этой цепи на угол 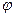 , причем
, причем  .
.
| 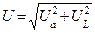
|
Мощность цепи:
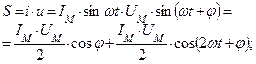
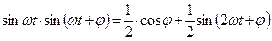
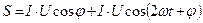
Т.о. мгновенная мощность состоит из двух составляющих: постоянной 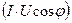 и переменной
и переменной  , среднее значение за период которой равно нулю.
, среднее значение за период которой равно нулю.
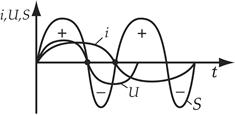
Мощность принимает как положительные так и отрицательный значения. Когда мощность положительна, то цепь потребляет энергию, а когда мощность отрицательна, то цепь возвращает запасенную энергию в цепь. Но т.к. потребляет энергию и активное сопротивление и индуктивное, а возвращает в цепь только индуктивность, то положительная будет значительно больше.
Треугольники напряжений, сопротивлений, мощностей

| 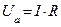  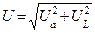
| Если стороны треугольника напряжений уменьшить или разделить на величину тока, то получим треугольник сопро-тивлений |

| 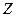 - полное сопротивление цепи - полное сопротивление цепи 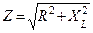
|

| - закон Ома для цепи с активным и индуктивным сопротивлением. |
Если стороны треугольника напряжений уменьшить на ток, то получим треугольник мощностей.

| 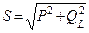 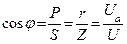 - коэффициент мощности - коэффициент мощности
|


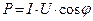 - реактивная мощность
- реактивная мощность
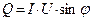 - активная мощность
- активная мощность
Коэффициент мощности показывает, какая часть полной мощности потребляется безвозвратно.
Цепь переменного тока с активным сопротивлением, емкостью и индуктивностью

| 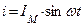 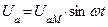 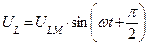 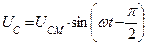 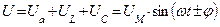
|
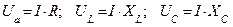
Допустим:
1. 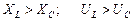

|  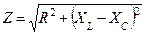 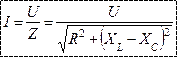 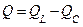 
|
2. 

|  
|
Общий случай неразветвленной цепи
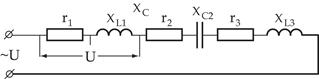

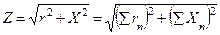
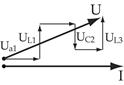
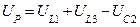
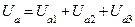
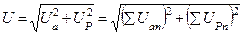
Резонанс напряжений
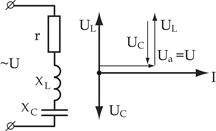
| 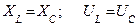 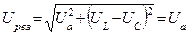 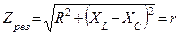 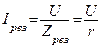
|
Результирующий ток  резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
резко увеличивается, т.к. индуктивное и емкостное сопротивления компенсируют друг друга.
Если параметры цепи подобрать так, что  , то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в
, то напряжения на емкости и индуктивности будут превышать напряжение на зажимах цепи в 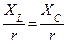 раз. Отношение
раз. Отношение 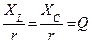 называется добротностью цепи (контура).
называется добротностью цепи (контура).
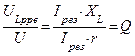

Т.о. напряжение на емкости и индуктивности будут превышать напряжение сети в 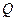 раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
раз, что может привести к пробою диэлектрика в конденсаторе или сопротивлений изоляции индуктивности, поэтому явление резонанса напряжений в электрических цепях нежелательно, но в то же время в радиотехнике его используют (колебательные контуры приемника и передатчика).
Возникновение напряжений на L и С, превышающих напряжение на зажимах цепи объясняется способностью емкости и индуктивности накапливать электрическую энергию.
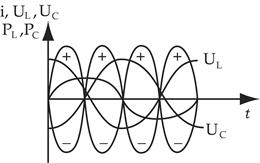
Между емкостью и индуктивностью происходит непрерывный обмен энергией, который называется собственными колебаниями.
Частоту собственных колебаний можно определить при условии, что  .
.
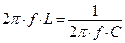 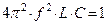 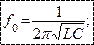
| Т.о. резонанс можно получить, изменяя частоту тока питающей сети, или изменяя емкость или индуктивность. 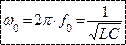
|
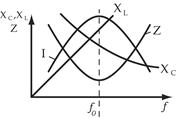
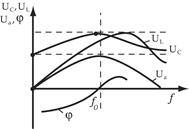
Резонансные кривые
Зависимость параметров цепи от частоты характеризуется резонансными кривыми.
| 
|
Разветвленные цепи переменного тока
Рассмотрим цепь с двумя параллельно соединенными катушками.

| 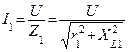 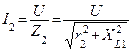
|
Для определения тока неразветвленной части цепи необходимо разложить токи  и
и 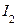 на активные и реактивные составляющие.
на активные и реактивные составляющие.

| 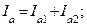  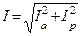
|
39) Характеристики синусоидальных величин: мгновенное, амплитудное, действующее, среднее значение, период, частота (угловая и циклическая), фаза
− мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u. Они являются функциями времени. Зависимость их от времени выражается соотношениями:
 ;
;
− фаза - аргумент синусоидальной функции (wt+j) - показывает, какое значение имеет синусоидальная функция в данный момент времени;
− начальная фаза j - показывает, какое значение имеет синусоидальная функция в момент на чала отсчета, т.е. при t=0;
− угловая (циклическая) частота изменения тока:
 , рад/c.
, рад/c.
Для нашей сети w=314 рад/c.
− Действующее значение переменного тока.
Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:

|
 .
.
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
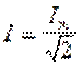 .
.
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
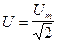
 .
.
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение фазного напряжения Um=UÖ2=307 В. Связь между действующим и амплитудным значениями напряжений важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
40)Цепи переменного тока с резистором: напряжение, ток, мощность, векторная диаграмма
Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол ?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах ?t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение. Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз ?, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Активная и реактивная мощности. Мгновенная мощность может быть представлена в виде суммы двух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).
Среднее ее значение, которое называют активной мощностью,
P = UI cos ? (75)
Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.
Составляющая 2 изменяется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным или емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, поэтому для оценки этой составляющей пользуются ее амплитудным значением, которое называют реактивной мощностью:
Q = UI sin ? (76)
Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю. Как видно из рис. 199,б, эта мощность становится то положительной, то отрицательной, т. е. соответствующая ей электрическая энергия ,3, называемая реактивной,
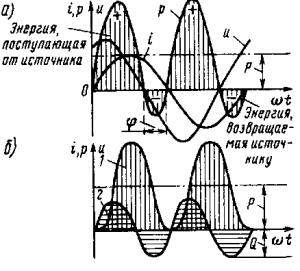 Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла ?t
Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла ?t
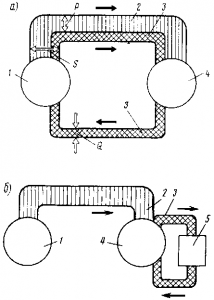 Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор
Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор
непрерывно циркулирует по электрической цепи от источника электрической энергии 1 к приемнику 4 и обратно (см. рис. 200, а).
Возникновение реактивной мощности в цепи переменного тока возможно только при включении в эту цепь накопителей энергии, таких как катушка индуктивности или конденсатор. В первом случае электрическая энергия, поступающая от источника, накапливается в электромагнитном поле катушки индуктивности, а затем отдается обратно; во втором случае она накапливается в электрическом поле конденсатора, а затем возвращается обратно к источнику. Постоянная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем самым не дает возможности использовать их по прямому назначению для выработки и передачи потребителям активной мощности. Поэтому в производственных условиях стараются по возможности уменьшить реактивную мощность, потребляемую электрическими установками.
Полная мощность. Источники электрической энергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток Iном и определенное номинальное напряжение Uном, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью,
S = UI
Следовательно, полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Связь между мощностями Р, Q и S можно определить из векторной диаграммы напряжений (рис. 201, а). Если умножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
S = ?(P2 + Q2)
Из этого выражения следует, что при заданной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока или трансформатор, тем меньше активная мощность Р, которую он может отдать приемнику. Иными словами, реактивная мощность не позволяет полностью использовать всю расчетную мощность источников переменного тока для выработки полезно используемой электрической энергии. То же самое относится и к электрическим сетям. Ток I = ?(Ia2+Ip2), который можно безопасно пропускать по данной электрической сети, определяется, главным образом, поперечным сечением ее проводов. Поэтому если часть Iр проходящего по сети тока (см. рис. 194,б) идет на создание реактивной мощности, то должен быть уменьшен активный ток Iа, обеспечивающий создание активной мощности, которую можно пропустить по данной сети.
 Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Если задана активная мощность Р, то при увеличении реактивной мощности Q возрастут реактивный ток Iр и общий ток I, проходящий по проводам генераторов переменного тока, трансформаторов, электрических сетей и приемников электрической энергии. При этом увеличиваются и потери мощности ?Р = I2Rпp в активном сопротивлении Rпp этих проводов.
Таким образом, бесполезная циркуляция электрической энергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, требует также затраты определенного количества энергии, которая теряется в проводах всей электрической цепи.
Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только от тока I и напряжения U, но и от величины cos?, называемой коэффициентом мощности:
cos ? = P/(UI) = P/S = P/?(P2 + Q2)
По значению cos ? можно судить, как использует мощность источника данный приемник или электрическая цепь. Чем больше cos ?, тем меньше sin ?, следовательно, согласно формулам (75) и (76) при заданных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos ? и постоянной активной мощности Р, поступающей в приемник, уменьшается ток в цепи I = P/(U cos ?). При этом уменьшаются потери мощности ?P = I2Rпp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. лучшего их использования. Если приемник питается от источника при неизменном токе нагрузки, то повышение cos ? ведет к возрастанию активной мощности Р, используемой приемником. При cos?=1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Поэтому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно повышать коэффициент мощности и доводить его по возможности до единицы.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cos? = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cos ? = 0,25-0,3).
Повышение коэффициента мощности. Cos ? повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов (статические компенсаторы), но могут быть применены также и синхронные электрические машины (вращающиеся компенсаторы).
Способ повышения cos ? с помощью статического компенсатора (рис. 202, а) называют компенсацией сдвига фаз, или компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i1 который отстает от напряжения и на некоторый угол сдвига фаз ?1. При включении компенсатора Хс по нему проходит ток ic, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при этом в цепи источника будет проходить ток i<i1 и угол сдвига фаз его ? относительно напряжения также будет меньше ?1.
Для полной компенсации угла сдвига фаз ?, т. е. для получения cos ? =1 и минимального значения тока Imin, необходимо, чтобы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin ?1 тока I1.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное повышение использования генераторов переменного тока и электрических сетей и уменьшение потерь энергии, возникающих при бесполезной циркуляции реактивной энергии между источником 1 и приемником 4. Компен-
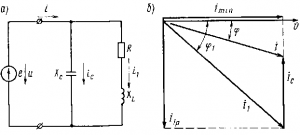 Рис. 202. Схема, иллюстрирующая способ повышения cos ? с помощью компенсатора (а), и векторная диаграмма (б)
Рис. 202. Схема, иллюстрирующая способ повышения cos ? с помощью компенсатора (а), и векторная диаграмма (б)
сатор в этом случае выполняет роль генератора реактивной энергии, так как токи Iсв конденсаторе и I1р в катушке индуктивности (см, рис. 202,б) направлены навстречу один другому (первый опережает по фазе напряжение на 90°, второй отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток Iр и сдвиг фаз между током I и напряжением U. При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos ? будет равен единице.
В большинстве случаев по экономическим соображениям в электрических установках осуществляют неполную компенсацию угла сдвига фаз и ограничиваются значением cos ? = 0,95.
41) Последовательное соединение активного и реактивного элементов
В общем случае в цепях переменного тока обычно имеются все виды сопротивлений: активное, индуктивное и емкостное. Например, электрические двигатели переменного тока могут быть представлены эквивалентной схемой, состоящей из индуктивного сопротивления имеющихся в нем катушек и активного сопротивления образующих эти катушки проводов. Воздушные линии элек-
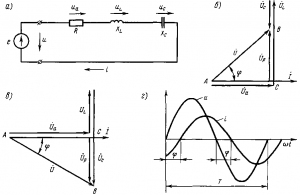 Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
Рис. 192. Схема цепи переменного тока, содержащей последовательно включенные активное, индуктивное и емкостное сопротивления (а), векторные диаграммы (б и а), кривые тока и напряжения и (г)
тропередачи или кабельные линии обычно представляют в виде совокупности активного, индуктивного и емкостного сопротивлений. Активное сопротивление обусловлено сопротивлением электрических проводов, индуктивное — индуктивностью линии, а емкостное — емкостью, возникающей между отдельными проводами, между проводами и землей или же между отдельными жилами кабеля и между жилами кабеля и его оболочкой.
Расчет электрических цепей переменного тока существенно отличается от расчета цепей постоянного тока, так как при переменном токе в активном, индуктивном и емкостном сопротивлениях имеют место различные сдвиги фаз между токами и напряжениями.
Ток, напряжение и полное сопротивление. При последовательном включении в цепь переменного тока активного R, индуктивного XL и емкостного Хс сопротивлений (рис. 192, а) к ним приложены напряжения: активное ua=iR, индуктивное uL = iXL и емкостное uc=iXc. Мгновенное значение напряжения и, приложенного к данной цепи, согласно второму закону Кирхгофа равно алгебраической сумме напряжений:
u = ua + uL + uc
Но для действующих значений эта формула неприменима, так как между всеми указанными напряжениями имеется сдвиг по фазе (амплитудные значения этих напряжений не совпадают по
 Рис. 193. Треугольник со противлении
Рис. 193. Треугольник со противлении
времени). Чтобы учесть сдвиг по фазе между напряжениями uа, uL и uc. осуществляют сложение их векторов:
? = ?a + ?L + ?C
Для этого строят векторную диаграмму, на которой откладывают в определенном масштабе векторы тока ? и напряжений ?a, ?L, ?C. Из этих напряжений первое совпадает по фазе с током, второе опережает его на 90°. Векторная диаграмма (рис. 192,б) построена для цепи, в которой индуктивное сопротивление XL больше емкостного Xc (вектор ?L, больше вектора ?C.), а рис. 192, в — для цепи, в которой XL меньше Хс (вектор ?L, меньше вектора ?C). Вектор напряжения U является замыкающим — он сдвинут по фазе относительно вектора тока ? на некоторый угол ?. Напряжение U (действующее значение) может быть определено из треугольника ЛВС по теореме Пифагора:
U = ?(U2a + (UL – Uc)2)
Таким образом, из-за наличия угла сдвига фаз ? напряжение U всегда меньше алгебраической суммы Ua + UL + UC. Разность UL – UC = Up называется реактивной составляющей напряжения.
Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.
В цепи, содержащей все три вида сопротивления, ток i и напряжение и оказываются сдвинутыми по фазе на некоторый угол ср (рис. 192, г), при этом 0<?<90°.
Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения Ua = IR; UL = l?L и UC=I/(?C), то будем иметь: U = ?((IR)2+ [I?L-I/ (?С) ]2), откуда получаем формулу закона Ома для последовательной цепи переменного тока:
I = U / (? (R2+ [?L-1 / (?С) ]2) ) = U / Z (72)
где Z = ? (R2+ [?L-1 / (?С) ]2) = ? (R2+ (XL – Xc)2)
Величину Z называют полным сопротивлением цепи, оно измеряется в омах. Разность ?L — l/(?C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Z = ? (R2+ X2)
Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис. 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.
Угол сдвига фаз ? определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:
sin ? = X / Z; cos? = R / Z; tg? = X / R
Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол ? сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз ? возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол ?; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол ?.
42) Идеальная катушка индуктивности, реальная катушка и конденсатор в цепи переменного тока.
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
Дата добавления: 2015-01-17; просмотров: 614; Мы поможем в написании вашей работы!; Нарушение авторских прав |