
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перевод правильной дроби из кода Д1 в двоичную систему счисления
Билет
1. Математической моделью систем с памятью является абстрактный автомат, определяемый как кортеж S=(A,Z,W,d,l, a0), у которого
· A={a0,a1, …, am, …, aM} - множество состояний (алфавит состояний), содержащее не менее двух элементов;
· Z={z1,z2, …, zF} - множество входных сигналов (входной алфавит);
· W={w1,w2, …, wG} - множество выходных сигналов (выходной алфавит);
· d : A´Z ®A - функция переходов, реализующая отображение пары "состояние - входной сигнал" в некоторое состояние автомата, т.е. d(am,zf) = as, am,as Î A;
· l : A´Z ® W - функция выходов для автомата Мили, она ставит в соответствие паре "состояние автомата - входной сигнал" некоторый выходной сигнал, т.е. l(am,zf) = wg;
· l : A®W функция выходов для автомата Мура, т.е. l(am)=wf, wf Î W;
· а0 - начальное состояние автомата.
Рисунок 2 Абстрактный автомат |
Абстрактный автомат, рис. 1, имеет один вход и один выход. Автомат работает в дискретном времени, принимающем целые неотрицательные значения t=0,1,2,… В каждый момент t дискретного времени автомат находится в некотором состоянии a(t) из множества состояний автомата А, причем в начальный момент он всегда находится в состоянии а0. В момент времени t автомат воспринимает на входе букву входного алфавита z(t)ÎZ, находясь в состоянии a(t). В соответствии с функцией переходов автомат переходит в момент времени (t+1) в состояние a(t+1)= d(a(t), z(t)) и вырабатывает выходной сигнал z(t) в соответствии с функцией выходов: z(t)=l(a(t), z(t)) в случае автомата Мили, и z(t)=l(a(t)) в случае автомата Мура. Таким образом, автомат S отображает множество слов входного алфавита Z в множество слов выходного алфавита W.
В абстрактном автомате мы отвлекаемся от его структуры, рассматривая его как "черный ящик" (принятый в кибернетике подход, когда основное внимание уделяется поведению системы относительно внешней среды).
Автомат называется конечным, если конечны множества A,Z,W. Далее мы будем рассматривать только конечные автоматы. Автомат называется полностью определенным, если он определен всюду на множестве A´Z. В противном случае автомат называется частичным.
Чтобы задать автомат, необходимо описать все компоненты вектора S=(A,Z,W,d,l, a0), т.е. входной и выходной алфавиты, алфавит состояний, функции переходов и выходов. Для описания автомата наиболее часто используются табличный и графический способы задания. Наиболее удобны отмеченные таблицы переходов-выходов, Таблицы 17, 18.
Таблица 18 Отмеченная таблица переходов-выходов для автомата Мили
Таблица 17 Таблица переходов-выходов для автомата Мура
|
Для частичных автоматов функции переходов и выходов определены не для всех пар (am,zf). В клетке неопределенности ставится прочерк.
Автомат называется детерминированным, если выполнено условие однозначности переходов. Автомат, заданный таблицей переходов, всегда детерминированный. В графе детерминированного автомата из одной вершины не могут выходить две и более дуги, отмеченные одним и тем же выходным сигналом.
Выделение в множестве состояний начального состояния объясняется чисто практическими соображениями, связанными с необходимостью фиксировать условия начала работы дискретного устройства. Автомат с выделенным начальным состоянием называется инициальным.
Если автомат задан таблицей или графом, задано входное слово из букв входного алфавита, то выходное слово однозначно определено, если существует последовательность состояний переходов автомата, обусловленная последовательностью входных сигналов. Последнее состояние в этом ряду, обусловленное приходом на вход последней буквы входного слова, называется заключительным состоянием автомата.
Выходной сигнал в автомате Мили зависит как от входного сигнала, так и от текущего состояния автомата. Поэтому, если заключительное состояние автомата определено, то выходной сигнал на последнюю букву входного слова появляется в момент появления этой буквы.
Перевод правильной дроби из кода Д1 в двоичную систему счисления
Перевод выполняется за n+1 такт, где n – число двоичных разрядов, обеспечивающих точность перевода такую же, как у исходного десятичного числа. Необходимое сило разрядов может быть определено из выражения
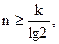 где k – число разрядов десятичного числа, определяющее его точность.
где k – число разрядов десятичного числа, определяющее его точность.
Чтобы определить алгоритм перевода числа из системы счисления с основанием q в систему счисления с основанием p, запишем числоAq в виде разложения по степеням 2:
Aq=a1p-1+a2p-2+…+anp-n=p-1(a1+p-1(a2+…+p-1(an+0))…).
(1)
Полученное выражение есть схема Горнера, определяющая последовательность действий при переводе.
Умножая Aq на p, получим смешанную дробь, целая часть которой будет равна первой цифре числа в системе счисления с основанием q. Далее, умножая дробную часть получившегося числа A’q на p, будем получать в целой части получающейся смешанной дроби значения очередных цифр в системе счисления с основанием р. При этом, если q>p, то цифры числа в новой системе счисления будут сразу получаться правильными. Если же p>q, то целая часть смешанной дроби, получающейся в результате умножения q-ичной правильной дроби на основание новой системы счисления будет представлять очередную цифру р-ичного числа кодовой последовательностью в q-ичной системе счисления. Из выражения (1) следует следующий алгоритм перевода правильной дроби из кода Д1 в двоичную систему счисления, представленный в табл. 1Примем значение исходного числа равным А10=0.13710. Число необходимых двоичных разрядов не меньше (3/lg2), т.е. больше или равно 10. Следовательно, необходимо принять число тактов равным 11 для последующего округления результата. В коде Д1 наше число будет иметь вид: А10= 0001 0011 0111. Умножение на 2 соответствует сдвигу регистра, в котором хранится число А на один разряд влево. Исходное число в коде Д1 хранится в РгА, Двоичный код записывается в РгВ последовательно разряд за разрядом, начиная со старшего разряда, путем сдвига РгВ влево. В таблице, представляющей алгоритм перевода, будем также записывать результат умножения десятичного числа на 2 в десятичной системе счисления (столбец А10), чтобы контролировать результат выполнения операций сдвига и коррекции в коде Д1. Таблица также содержит столбец СТ, в котором учитывается число уже выполненных тактов. Критерием завершения операции перевода является СТ=0.
Таблица 13 Перевод правильных дробей из кода Д1 в двоичную систему счисления
| РгВ | РгА | А10 | CT | Комментарии |
| ***** ****** | 0.00001 0011 0111 | 0.137 | Загрузить [A] в РгА. СТ:=11, РгВ:=0, | |
| ***** *****0 | 0.0010 0110 1110 | 0.274 | РгВ[10]:=РгА[0], РгА:=L(1)РгA, | |
| 0.0010 0111 0100 | Выполнить коррекцию в тетрадах. Сравнить полученный результат с вычисленным значением А10. | |||
| ***** ****0* | 0.0100 1110 1000 | 0.548 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 0.0101 0100 1000 | Выполнить коррекцию тетрад. | |||
| ***** ***00* | 0.1010 1001 0000 | 1.096 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 1.0000 1001 0110 | Выполнить коррекцию тетрад | |||
| ***** **001* | 0.0001 0010 1100 | 0.192 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 0.0001 1001 0010 | Выполнить коррекцию тетрад | |||
| ***** *0010* | 0.0011 0010 0100 | 0.384 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 0.0011 1000 0100 | Выполнить коррекцию тетрад | |||
| ***** 00100* | 0.0111 0000 1000 | 0.768 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 0.0111 0110 1000 | Выполнить коррекцию тетрад | |||
| ****0 01000* | 0.1110 1101 0000 | 1.536 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 1.0101 0011 0110 | Коррекция тетрад | |||
| ***00 10001* | 0.1010 0110 1100 | 1.072 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 1.0000 0111 0010 | Коррекция тетрад | |||
| **001 00011* | 0.0000 1110 0100 | 0.144 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 0.0001 0100 0100 | Коррекция тетрад | |||
| *0010 10110* | 0.0010 1000 1000 | 0.288 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| Коррекция тетрад не требуется | ||||
| 00100 01100* | 0.0101 0001 0000 | 0.576 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 0.0101 0111 0110 | Коррекция тетрад | |||
| 00101 011000 | 0.1010 1110 1100 | 1.152 | РгВ[10]:=РгА[0], РгВ:=L(1)РгВ, РгА:=L(1)РгА, СТ:=СТ-1, | |
| 1.0001 0101 0010 | ||||
| 00100 011000 + 1 00100 011001 | СТ=0? ДА Выход из цикла. Округление СМ:=СМ+1, | |||
| ШД:=РгB[0:10] – выдача результата в шину данных (ШД). |
Результат получается отбрасыванием младшего разряда суммы после округления.
Таким образом схема операционного автомата должна содержать двенадцатиразрядный РгА, одиннадцатиразрядный РгВ, счетчик числа циклов СТ и сумматор для выполнения округления. В этом случае нет необходимости в использовании полного двоичного сумматора. Поэтому можно применить комбинационную схему, выполняющую подсуммирование 1 в младший разряд полученного двоичного числа. Следует иметь в виду, что запятая в данном случае фиксирована слева от старшего разряда.
Коррекции в коде Д1 при сдвиге влево выполняются:
- при получении недопустимой тетрады;
- в младшей тетраде при наличии передачи единицы из младшей тетрады в старшую,
- коррекция в тетраде выполняется только один раз; т.е., если при коррекции возникает перенос в старшую тетраду, он не требует коррекции.
В любом случае коррекция в коде Д1 состоит в подсуммировании +6 к тетраде, требующей коррекции. При коррекции формируется символ переноса в старшую тетраду. Поэтому запись цифры из целой части дроби в коде Д1 в РгВ [10] следует производить после выполнения коррекции.



Дата добавления: 2015-01-19; просмотров: 286; Мы поможем в написании вашей работы!; Нарушение авторских прав |
