Представление чисел со знаком в ЭВМ

Для кодирования знака используется один бит, который принимается равным 0 в случае положительного числа, и 1 – отрицательного. В формате регистра знаковому разряду отводится определенное место. Для представления чисел со знаком применяют три вида кодов. Правило записи чисел со знаком не зависит от того, в каком месте фиксирована запятая. Мы будем в дальнейшем подразумевать, что запятая фиксирована слева от старшего разряда, имея в виду, что при выполнении действий с плавающей запятой операции сложения, умножения, деления выполняются над мантиссами, а порядки в соответствии с логикой операции выравниваются, складываются или вычитаются.

Прямой код представляет числа со знаком в соответствии с правилом:

Например, [0,1101]_П=0,1101; [-0,1101]_П=1,1101. Знаковый разряд несет в случае прямого кода смысловую, но не арифметическую нагрузку и не может участвовать в подсуммированиях. Алгебраическое сложение в прямом коде невозможно. Поэтому прямой код, как правило, не применяется для выполнения арифметических операций.

Дополнительный код:

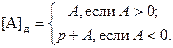где p – основание системы счисления.

Основание любой системы счисления представляется как 10. Пусть А=-0,1101. Дополнительный код определится следующим образом:

10,0000

-0,1101

1,0011 - это дополнительный код числа А. Чтобы получить его, достаточно инвертировать все цифры в естественной записи числа, включая знаковый разряд, до последней значащей цифры. Последняя значащая цифра не инвертируется. Знаковая цифра в дополнительном коде имеет вес 2⁰=1. Поэтому он может принимать участие в выполнении арифметических операций наравне с числовыми разрядами. Дополнительный код позволяет выполнять операции алгебраического сложения. Результат при этом получается автоматически с правильным знаком. Если при сложении со знакового разряда спадает 1, она теряется.

Обратный код образует код числа в соответствии с правилом:

где n – количество числовых разрядов, p – основание системы счисления.

Для представления отрицательного двоичного числа в обратном коде достаточно инвертировать все цифры в естественной записи числа, включая знаковую цифру. Например,

[-0,1101]_О = 1,0010; [0,1101]_О = 0,1101.

Знаковый разряд в обратном коде, так же, как в дополнительном, имеет вес 1 и участвует в подсуммированиях наравне с числовыми разрядами. Из правила образования обратного кода следует, что для получения дополнительного кода отрицательного двоичного числа достаточно прибавить 1 в младший разряд его обратного кода.

Алгебраическое сложение двоичных чисел в обратном коде дает автоматически результат с правильным знаком.

Сформулированные правила справедливы для любой системы счисления. Необходимо иметь в виду, что в системе счисления с любым основанием разряды, занимающие позиции знакового разряда (слева от старшего разряда числа), складываются как двоичные.