
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Движение тела в неинерциальных системах отсчета. Проявление поступательной силы инерции. Принцип эквивалентности.
Неинерциальные системы отсчета (НСО) −системы отсчета, для которых не выполняется первый закон Ньютона (системы отсчета, которые движутся с ускорением  относительно любой инерциальной системы отсчета).
относительно любой инерциальной системы отсчета).
При описании движения материальной точки (тела) в неинерциальной системе отсчета наряду с реально действующими на тело силами рассматриваются силы инерции. Все силы инерции имеют следующие общие свойства:
1. Они обусловлены не взаимодействием тел, а свойствами самих неинерциальных систем отсчета. Поэтому на силы инерции третий закон Ньютона не распространяется.
2. Существуют только в неинерциальных системах отсчета.
3. Все силы инерции, подобно силам тяготения, пропорциональны массе  тела.
тела.
Основное уравнение динамики в неинерциальных системах отсчета  , где
, где  − масса тела;
− масса тела;  − ускорение тело в неинерциальной системе отсчета
− ускорение тело в неинерциальной системе отсчета  ;
;  − постоянная угловая скорость, с которой вращается неинерциальная система
− постоянная угловая скорость, с которой вращается неинерциальная система  вокруг оси, перемещающейся поступательно с ускорением
вокруг оси, перемещающейся поступательно с ускорением  относительно инерциальной системы
относительно инерциальной системы 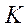 ;
; 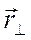 − оставляющая радиус-вектора, перпендикулярная оси вращении и характеризующая положение частицы относительно этой оси;
− оставляющая радиус-вектора, перпендикулярная оси вращении и характеризующая положение частицы относительно этой оси;  − скорость тела относительно неинерциальной системы
− скорость тела относительно неинерциальной системы  .
.
Поступательная сила инерции, обусловленная поступательным движением неинерциальной системы отсчета с ускорением 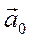 :
:  .
.
Принцип эквивалентности: из равенства инертная масса = гравитационной массе тела следует, что система отсчета движетсяпоступательно с ускорение 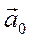 в отсутствии поля тяжести все физические процессы происходят так же, как и в неподвижной системе отсчета находящейся в соответв. поле тяготения (с ускорением свободного падения равному ускорению системы
в отсутствии поля тяжести все физические процессы происходят так же, как и в неподвижной системе отсчета находящейся в соответв. поле тяготения (с ускорением свободного падения равному ускорению системы 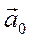 ), т.е. находясь в закрытой системе (т.е. не имея внешних ориентиров) никакими физическими экспериментами невозможно определить, движется данная система с ускорением
), т.е. находясь в закрытой системе (т.е. не имея внешних ориентиров) никакими физическими экспериментами невозможно определить, движется данная система с ускорением 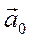 или находится в поле тяготения. В этом и состоит принцип эквивалентности: система отсчета движется с ускорением неотличимо от присутствия соответственного однородного поля тяготения.
или находится в поле тяготения. В этом и состоит принцип эквивалентности: система отсчета движется с ускорением неотличимо от присутствия соответственного однородного поля тяготения.
Кинематика абсолютно твердого тела. Поступательное и вращательное движение. Углы Эйлера. Плоское движение твердого тела.
Кинетическая энергия вращающегося тела:  , где
, где 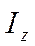 − момент инерции твердого тела относительно неподвижной оси вращения
− момент инерции твердого тела относительно неподвижной оси вращения  ;
; 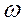 − угловая скорость вращения тела.
− угловая скорость вращения тела.
Кинетическая энергия поступательного движения твердого тела: 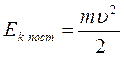 , где
, где  − масса твердого тела;
− масса твердого тела;  − скорость поступательного движения тела.
− скорость поступательного движения тела.
Полная кинетическая энергия твердого тела  равна сумме кинетической энергии вращательного и кинетической энергии поступательного движения тела:
равна сумме кинетической энергии вращательного и кинетической энергии поступательного движения тела: 
Для описания вращения твердого тела вводятся угловые координаты – углы Эйлера.При вращении твердого тела вокруг точки О, поворот описывается 3-мя углами: угол нутации, угол прецессии и угол собственного вращения.
Плоское движение АТТ – движение тела, при котором траектории всех его точек лежат в параллельных плоскостях. Для плоского движения выполняется следствие из т. Эйлера – при плоском движении переход твердого тела из одного произвольного состояния в другое может быть осуществлен одним поворотом вокруг мгновенной оси движения.
Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Свободные оси вращения твердого тела. Закон сохранения момента импульса.
Момент импульса твердого тела 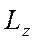 относительно неподвижной оси вращения −величина, равная произведению момента инерции тела
относительно неподвижной оси вращения −величина, равная произведению момента инерции тела  относительно неподвижной оси вращения
относительно неподвижной оси вращения  и угловой скорости вращения
и угловой скорости вращения  тела:
тела:  .
.
Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:  , произведение момента инерции твердого тела
, произведение момента инерции твердого тела  относительно неподвижной оси вращения
относительно неподвижной оси вращения  на угловое ускорение
на угловое ускорение  тела равно моменту сил
тела равно моменту сил 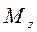 , действующих на тело относительно этой оси:
, действующих на тело относительно этой оси:
Закон сохранения момента импульса −суммарный момент импульса замкнутой системы материальных точек не изменяется с течением времени:  .
.
Свободные оси вращения – оси, которые без специального закрепления сохраняют свое направление в пространстве.
Дата добавления: 2015-01-19; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |