Место логики в методологии научного познания. Методологические принципы познания. Понятие о методах, принципах и приемах познания.

Определение предмета и содержание науки логики. Объективная и субъективная логики, логика как предмет.

Логика -- наука о мышлении. Но в отличие от других наук, изучающих мышление человека, например физиологии высшей нервной деятельности или психологии, логика изучает мышление как средство познания; ее предметом являются законы и формы, приемы и операции мышления, с помощью которых человек познает окружающий его мир.

Субъективная логика- это логика понятия сущности, которая сняла свое отношение к некоторому бытию или, иначе говоря, к своей видимости и которая теперь уже не внешняя в своем определении, а есть свободное, самостоятельное, определяющее себя внутри себя субъективное, или, вернее, есть сам субъект. Так как выражение "субъективное" приводит к недоразумениям, поскольку оно может быть понято в смысле чего то случайного и произвольного, равно как вообще в смысле определений, относящихся к форме сознания, то не следует здесь придавать особое значение различию между субъективным и объективным, которое позднее будет более подробно разъяснено при изложении самой логики. Логикой называют закономерности в изменении и развитии вещей и явлений объективного мира. Это объективная логика.

2.Мышление как логический процесс: чувственное познание и абстрактное мышление. Особенности абстрактного мышления.Всякое познание начинается с живого созерцания. Предметы воздействуют на наши органы чувств и вызывают в мозгу ощущения, восприятия, представления, которые являются формами чувственного познания. Ощущение – это отражение отдельных свойств предметов или явлений материального мира, непосредственно воздействующих на органы чувств (например: отражение свойств горького, сладкого, теплого и т. д.).Восприятие есть целостное отражение внешнего материального предмета, непосредственно воздействующего на органы чувств (например: образ автобуса, пшеничного поля и т.д.).Представление – это чувственный образ предмета, в данный момент нами не воспринимаемого, но воспринятого ранее в той или иной форме. Примерами воспроизводящего представления являются образы своего дома, образы наших знакомых и родных. Представление может быть не только воспроизводящим, но и творческим, но и в том числе фантастическим.Путем чувственного отражения мы познаем отдельные предметы и их свойства. Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления, более сложной формы познания. Абстрактное или рациональное мышление отражает мир и его процессы глубже и полнее, чем чувственное познание.Основными формами абстрактного мышления являются понятия, суждения, и умозаключения.Понятие – форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов.Суждение – форма мышления, в которой что-либо утверждается или отрицается о предметах, их признаках и отношениях. Суждение выражается в форме повествовательного предложения. Суждения могут быть простыми и сложными.Умозаключение- форма мышления, посредством которой из одного или нескольких истинных суждений, называемых посылками мы по определенным правилам вывода получаем заключение.

Содержание и формы мышления. Понятие о логической форме мысли. Основные логические формы мысли.

Содержание мышления - то, о чем человек думает, размышляет .Объектом мыслей, рассуждений может быть все, что существует во Вселенной, а также созданное самим творческим мышлением человека Предмет мыслей (соображений), который вв водится в сферу абстрактно-логического, рационального мышления определяется как абстрактный объкт.

Форма мышления - это структура мыслительной деятельности людей, сложившейся исторически в процессе отражения предметов, явлений, процессов объективного мира в их взаимосвязи, способ организации содержания

Мышление человека протекает в форме суждений и умозаключений. Суждение — это форма мышления, отражающая объекты действительности в их связях и отношениях. Каждое суждение есть отдельная мысль о чём-либо. Последовательная логическая связь нескольких суждений, необходимая для того, чтобы решить какую-либо мыслительную задачу, понять что-нибудь, найти ответ на вопрос, называется рассуждением. Рассуждение имеет практический смысл лишь тогда, когда оно приводит к определённому выводу, умозаключению. Умозаключение и будет ответом на вопрос, итогом поисков мысли.

Умозаключение — это вывод из нескольких суждений, дающий нам новое знание о предметах и явлениях объективного мира. Умозаключения бывают индуктивные, дедуктивные и по аналогии.

Логическая форма мысли-есть общее, объединяющее понятия, суждения или умозаключения, несмотря на то, что в них говорится о разных предметах.

В естественном языке мысли выражаются с помощью слов и словосочетаний и имеют конкретное содержание (то, о чем в них говорится). Отвлекаясь от конкретных предметов, человек обобщает их в классы. Предметы обобщаются в классы, так как они имеют общие свойства. Например, общее свойство космонавтов – «быть человеком, который летал в космос», свойство стола – «быть предметом домашней мебели, представляющим собою широкую поверхность из досок (деревянных, мраморных и др.), укрепленных на одной или нескольких ножках и служащий для того, чтобы ставить или класть что-нибудь» и т.д. Если отвлечься от специфики этих свойств, объединить их и обозначить, например, символом А. Тогда связь между классами предметов и классом общих свойств этих предметов можно представить следующей формулой: X A (X) (класс таких предметов X, которые обладают признаками А). Логиче-ская форма понятий – это способ связи между классом предметов и совокупностью признаков предметов этого класса.

Логическая форма суждений – это способ связи понятий о предмете, о свойствах предметов или отношений между предметами, выраженный в форме утверждения или отрицания. Например, возьмем три суждения: «Все школьники – учащиеся», «Все люди смертны» и «Все русские любят быструю езду». Отвлекаясь от свойств, приписываемых субъекту, заменим их символом Р (предикат). Тогда все эти суждения будут иметь одинаковую форму: Все S суть Р, которая и является логической формой суждений.

Логическая форма умозаключений – это способ связи суждений, так что из истинных суждений необходимо следуют другие истинные суждения .

При выявлении логической формы сохраняется информация о том, к какой семантической категории (классу выражения языка) относится термин, заменяемый переменной. Поэтому в логике предикатов для выражения разных категорий вводятся различные символы. При выявлении логической формы различные вхождения одного и того де термина в контекст заменяются одной и той же буквой, а различные термины – разными буквами .

Выделяют три логические формы или формы мышления:

1. Понятие.

2. Суждение

3. Умозаключение

Понятие – это форма мышления, с помощью которой создаются мысленные образы предметов, представления об их свойствах и отношениях.

Суждение — форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами.

УМОЗАКЛЮЧЕНИЕ — умственное действие, связывающее в ряд посылок и следствий мысли различного содержания

4,5 Понятие о языке. Виды языков. Семиотика как наука о языке и ее основные разделы.

Чарльз Пирс – американский ученый, философ, жил во 2 половине 19 в., с ним связано становление семиотики как науки. Знак-нечто, заменяющее для кого-то что-то в каком-либо отношении.Семио́тика, или семиоло́гия (греч. σημειωτική, от др.-греч. σημεῖον — «знак, признак»), — наука, исследующая свойства знаков и знаковых систем (естественных и искусственных языков).Знак – двусторонняя сущность. В языке знаки: морфемы, слова и предложение (фонемы – это не знаки). Стороны – внешняя (звуковая оболочка - означающее) и внутренняя (то, что данная оболочка называет - означаемое).Под знаковой системой понимается набор знаков - одного типа или же нескольких типов вместе с системой правил, регулирующих сочетаемость знаков при создании семиотического текста.Язык – открытая, первичная знаковая система (остальные вторичны, т.е. либо все остальные системы возникли на базе человеческого языка, либо могут быть объяснены с его помощью).Системы аналогичные человеческому языку (азбука Морзе, шрифт Брайля, язык глухонемых), знаковые системы для общения животных (нет синтаксиса, синонимии и омонимии), знаковые системы, связанные с искусством (кино, музыка, танец).Возможны различные классификации знаковых систем, например, по функции их употребления: 1) коммуникативными (естественные языки, искусственные языки, разные виды искусства, игры) или же 2) некоммуникативными(восприятие, группа нормативных систем типа юридических знаков, этических норм и т.д.).Знаковые системы можно разделить на 1) информационные и 2) неинформационные (игра в шахматы). Можно также говорить о знаках звуковых (вокальных, аудитивных), зрительных, тактильных.Существуют как естественные (спонтанно возникшие), так и искусственные коммуникативные системы (письмо, системы символов в физике, математике и т.д.)Знаки, из которых строятся сообщения, играют роль носителей определенных смысловых содержаний (значений). Знак = понятие + акустический образ.Знак существует для того, чтобы по его средствам назвать, обозначить денотант, т.е. выделенный сознанием предмет, действие, состояние и многое другое.Пирс первым описал различные знаковые системы, исследовал свойства и отношения знаков, дал их классификацию на основе реалий, обозначаемых этими знакам. Пирс описал 3 типа знаков:Типы знаков (Пирс):1) знаки-иконы: связаны с обозначаемым объектом (фотографии, изображения, образы(туалет-фигура ж/м));2) знаки-индексы: характеризуются смежностью с реалией, основаны на физич связи с объектом –стук в дверь (гром – где-то идет гроза, дым – где-то пожар, флюгер-направление ветра);3) знаки-символы: условные знаки. Не мотивированы(М/Ж)Последователь Пирса(отец семиотики)-Моррис-создал семиотику. У морриса знак-сумма условий, достаточных д/ его формирования:1.наличие знаконосителя (след)2.десигнат-то, на что знак указывает, к чему относится (след зайца)3.воздействие- как воздействует з на интерпритатора-реакция4.интерпритатор-выводы (след зайца)Особенность знака в том, что с ним искусственно связана некоторая информация, несвязанная со структурными и функциональными свойствами знака как объекта. Знак выступает как носитель информации, представляющий любой предмет.Наука о знаке предполагает разделы, Е 3 раздела:1) семантика – рассматривает отношение знаков к обозначаемому; смысл знаков,2) синтактика – соотношение знаков между собой,3) прагматика – изучает взаимодействие знака и человека «адресата»; в разных условиях значения знака может быть разное; ситуация и условие влияют на семантику слова.Свойства знаков (Соссюр):1.знак – материальная и идеальная сущность одновременно. Материальное – означаемое (понятие), идеально – означающее (акустический образ);2.ассиметричность: отношения между означаемым и означающим ассиметричны (омонимия и синонимия);3.произвольность знака: отсутствие связи/отношений между означающим и означаемым (понятие не связано внутр отнашением со звук образом бык-ox, beuf-что правильно);4.мотивированность: слово «сорок» – не мотивировано, а вот внутренняя форма слова пятьдесят прозрачна (пять + десять), существование мотивированных слов облегчает овладение языком;

1. .перцептивность: знак должен быть доступен восприятию со стороны адресата;

2. .информативности: знак должен нести смысловую информацию об объекте;

3. .стабильность/вариативность(изменчивость/не)

- может меняться означающее при сохранении означаемого;- может меняться означаемое при сохранении означающего;- может происходить ухудшение и улучшение значения.

Место логики в методологии научного познания. Методологические принципы познания. Понятие о методах, принципах и приемах познания.

Логика выполняет в научном познании ряд функций. Одной из них является методологическая. Чтобы описать эту функцию, нужно охарактеризовать понятие методологии.Слово “методология” состоит из слов “метод” и “логия”. Последнее, находясь в конце сложного слова, означает “учение”. То есть буквально методология — это учение о методе. Употребляется это слово в двух смыслах: во-первых, методологией называют систему нематериальных средств познания и преобразования действительности; во-вторых, — учение о нематериальных средствах познания и преобразования действительности. Такая двуплановость научных понятий — явление обычное. Так, логикой называют особые закономерности в связях и развитии мыслей, а также науку об этих закономерностях.Основными нематериальными средствами познания и преобразования действительности (методологическими средствами) являются принципы, методы, приемы и некоторые другие.Методологические принципы следует отличать от мировоззренческих. Для уяснения этого необходимо иметь в виду, что в науке различают две стороны: дескриптивную (описывающую) и прескриптивную (предписывающую). Мировоззрение является дескриптивной стороной науки, а методология — прескриптивной. Мировоззрение в широком смысле слова — это система взглядов на мир(на природу, общество и познание). Основу мировоззрения образует философское мировоззрение, называемое иногда мировоззрением в узком смысле слова. Мировоззрение составляют: принципы (мировоззренческие), представляющие собой знания о наиболее общих связях и свойствах объективной действительности и познания (наиболее общие в рамках предметной области конкретной науки — тогда это принципы конкретной науки, и наиболее общие безотносительно к конкретной науке — тогда это философские принципы); законы — знания об особых связях в объективной действительности и познании, менее общих, чем первые (в рамках предметной области той или иной науки), и категории.В отличие от мировоззренческих принципов принципы познания и практической деятельности (методологические принципы} представляют собой наиболее общие предписания, указывающие, как следует осуществлять познание и практическую деятельность. Методологические принципы вырабатываются чаще всего на основе мировоззренческих принципов, а также на основе законов в процессе познания и практики. Например, в философии на основе мировоззренческого принципа первичности материального и вторичности идеального разработан методологический принцип объективности рассмотрения, предписывающий, в частности, в социальном познании идти не от вторичных явлений к причинам, а, наоборот, из причин выводить соответствующие следствия.Слово “метод” в научной литературе употребляется в двух смыслах. Во-первых, методом называют всю систему нематериальных средств познания и преобразования действительности, т.е. методологию в целом. В этом смысле употребляют слово “метод”, когда говорят о диалектическом методе, о методе теоретической физики, о методе Бэкона и т.д.Во втором смысле метод (метод как элемент методологии) можно определить как способ познавательной или практической деятельности, представляющий собой последовательность познавательных операций, или этапов деятельности, выполнение которых (в указанной последовательности) способствует наиболее успешному достижению желаемого результата. Наиболее общие методы, прежде всего философские, указывают общее направление познания, которое конкретизируется последовательным применением методов меньшей степени общности. Применение наиболее частных методов — алгоритмов с необходимостью приводит к желаемому результату. Эти методы представляют собой точные предписания, которые определяют процесс теоретической или практической деятельности, ведущий от исходных данных к желаемому результату.Приемы, тоже являющиеся компонентами методологии, представляют собой относительно несложные способы познавательной или практической деятельности, которые помогают успешному достижению поставленной цели и, как правило, выступают частью какого-либо метода.Между принципами, методами и приемами познания трудно провести абсолютные границы. Например, наиболее простые методы можно считать приемами познавательной или практической деятельности и наоборот.Логическая методология включает в себя методологические средства формальной логики и методологические средства диалектической логики.Принципы, методы и приемы диалектической логики являются наиболее общими, в указанном выше смысле, или всеобщими. Научное познание, как правило, начинается с применения принципов, методов и приемов диалектической логики, указывающих общее направление исследования. Особую роль в методологии научного познания выполняют формы развития знания. Они выступают в качестве средства, организующего последовательность применения принципов, методов и приемов познания. Принципы, методы и приемы формальной логики, не являясь всеобщими в указанном выше смысле, действуют на всем протяжении процесса познания и играют роль общей методологии, обеспечивая возможность применения любых других методологических средств, в том числе и всеобщих.Некоторые методы и приемы формальной логики, особенно методы и приемы логики символической, выполняют в социальном познании роль частнонаучных методологических средств. Таковыми, например, являются методы алгебры логики, применяемые для нахождения наилучшей формулировки управленческого решения.

7. Диалектическая логика: ее специфика и основные принципы. Их место в методологическом инструментарии науки.

Диалектика (греч. dialektike) - наука о наиболее общих законах развития природы, общества и мышления. Уже античная философия акцентировала внимание на изменчивости всего существующего. Действительность понималась как процесс перехода всякого свойства в противоположное (Гераклит, пифагорейцы). К подобным исследованиям еще не применялся термин «диалектика». Первоначально этим термином обозначалось искусство диалога и спора. Платон определяет истинное бытие как тождественное и неизменное. Тем не менее он обосновывал диалектические выводы о том, что высшие роды сущего могут мыслиться только так, что каждый из них есть и не есть, равен себе самому и не равен, тождествен себе и переходит в свое «иное».Противоречие есть необходимое условие для побуждения души к размышлению. Это искусство и является, по Платону, искусством диалектики.Развитие диалектики продолжали неоплатоники (Плотин, Прокл). В философии феодального общества (схоластике) диалектикой стали называть формальную логику, которая была противопоставлена риторике.В эпоху Возрождения диалектические идеи о «совпадении противоположностей» выдвигают Н. Кузанскийи, Дж. Бруно. В Новое время, несмотря на засилье метафизики, Р. Декарт и Б. Спиноза (первый - в своей космогонии, второй - в учении о субстанции как о самопричине) дают образцы диалектического мышления. В XVIII в. во Франции богатством диалектических идей выделяются Ж. Ж. Руссо и Д. Дидро. В теории познания И. Сайг развивает диалектические идеи в учении об «антиномиях». И. Фихте развивает «антитетический» метод выведения категорий, содержащий важные диалектические идеи. Вершиной в развитии домарксистской диалектики была идеалистическая диалектика Г. В.Ф. Гегеля. Диалектика, по его мнению, - «движущая душа всякого научного развертывания мысли, представляет собою принцип, который один вносит в содержание науки имманентную связь и необходимость».

Зрелое научное понимание диалектики создано К. Марксом и Ф. Энгельсом. Они построили диалектику на основе материалистического понимания исторического процесса и развития познания, обобщения реальных процессов, происходящих в природе, обществе и мышлении. В научной диалектике сочетаются законы развития и бытия, и познания, так как они тождественные по своему содержанию и отличаются только по форме.Материалистическая диалектика не только «онтологическое», но и гносеологическое учение, логика, рассматривающая мышление и познание одинаково в становлении и развитии, поскольку вещи и явления есть то, чем они становятся в процессе развития, и в них, как тенденция, заложено то, чем они станут.Главной категорией материалистической диалектики является Противоречие. В учении о противоречиях она раскрывает движущую силу и источник всякого развития. В нем содержится ключ к остальным категориям и принципам диалектического развития: к развитию путем перехода количественных изменений в качественные, к перерыву постепенности, отрицанию исходного момента развития и отрицанию этого отрицания, повторению на высшем уровне некоторых сторон первоначального состояния.

8. Диалектическая логика: ее специфика и основные принципы. Их место в методологическом инструментарии науки.

Первый закон логики- закон тождества - гласит: "Каждая мысль в процессе данного рассуждения должна иметь одно и то же определенное, устойчивое содержание". Это значит, что во время рассуждения нельзя подменять один предмет мысли другим.Следующий логический закон- закон противоречия: "Две противоположные мысли об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, не могут быть одновременно истинными". По мнению исследователей, впервые этот закон был сформулирован Аристотелем. Закон противоречия он считал основным принципом мышления. Против непоследовательности в наших рассуждениях направлен и закон исключенного третьего. Он гласит: "Из двух противоречащих высказываний в одно и то же время и в одном и том же отношении одно непременно истинно". Этот закон, как и предыдущий, был сформулирован Аристотелем. Латинская формулировка этого закона звучит так: "Третьего не дано" (tertium non datur). Правильное мышление должно быть не только определенным, последовательным и непротиворечивым, но также и доказательным. Этого требует закон достаточного основания: "Всякая правильная мысль должна быть обоснована другими мыслями, истинность которых доказана". Этот закон был сформулирован немецким мыслителем Лейбницем. Он выразил его в виде следующего принципа: "Все существующее имеет достаточное основание для своего существования".Закон достаточного основания отражает важнейшую особенность окружающего мира: в природе и обществе все взаимосвязано и взаимообусловлено. Ни одно явление не может произойти, если оно не подготовлено предшествующим развитием.Закон достаточного основания не допускает голословности утверждений и выводов, требует убедительного подтверждения истинности наших мыслей. Обоснованность высказываний - важнейшее требование, предъявляемое к речи.Формально-логические законы - это законы правильного мышления, соблюдение которых делает рассуждения ясными, четкими, последовательными и непротиворечивыми, обоснованными и доказательными.Что касается видов доказательства, то различают доказательства прямые и косвенные.При прямом доказательстве тезис обосновывается аргументами без помощи дополнительных построений. Например: Данное учебное заведение действительно является крупнейшим университетом нашего города. Именно в этом вузе преподают многие известные ученые города, высокий процент выпускников этого вуза составляет коммерческую и научную элиту Новосибирска. Материально-техническая база университета впечатляет: лаборатории, оснащенные современным оборудованием, обилие компьютерных классов, богатейшая библиотека, фонды которой постоянно пополняются, новый спорткомплекс и т. п.Косвенное доказательство предполагает обоснование истинности тезиса посредством опровержения противоречащего положения - антитезиса. Из ложности антитезиса на основании закона исключенного третьего делается заключение об истинности тезиса. Например: Мне довелось недавно услышать мнение, что данное учебное заведение не соответствует статусу университета. Действительно, сегодня нелегкие времена переживают некоторые вузы… Однако в результате последней государственной аттестации этого вуза в очередной раз подтвердилось, что именно в этих стенах преподают многие известные ученые города, высокий процент выпускников этого вуза составляет коммерческую и научную элиту Новосибирска. Материально-технической базе этого учебного заведения могли бы позавидовать другие вузы: лаборатории, оснащенные современным оборудованием, обилие компьютерных классов, богатейшая библиотека, фонды которой постоянно пополняются, новый спорткомплекс и т.п. Безусловно, эти объективные характеристики позволяют считать данное учебное заведение университетом.

Закон тождества, закон непротиворечия, закон исключенного третьего как основные законы формальной логики, выражающие требования определенности и последовательности мышления. Их смысл и запись на языке логики предикатов.

Зако́н то́ждества — закон логики, согласно которому в процессе рассуждения каждое осмысленное выражение (понятие, суждение) должно употребляться в одном и том же смысле. Предпосылкой его выполнимости является возможность различения и отождествления тех объектов, о которых идёт речь в данном рассуждении.[1] Мысль о предмете должна иметь определённое, устойчивое содержание, сколько бы раз она ни повторялась. Важнейшее свойство мышления — его определённость — выражается данным логическим законом. Закон непротиворечия (закон противоречия) — закон логики, который гласит, что два несовместимых (противоречащих) суждения не могут быть одновременно истинными. По крайней мере, одно из них ложно[1].Математическая запись:

где 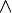— знак конъюнкции, — знак отрицания.

Закон противоречия является фундаментальным логическим законом, на котором построена вся современная математика. Он является тавтологией классической логики, а также большинства неклассических логик, в том числе интуиционистской логики. Всё же, существуют нетривиальные логические системы, в которых он не соблюдается, например логика Клини.Закон противоречия говорит о том, что если одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте, в одно и то же время и в одном и том же отношении, то они не могут быть одновременно истинными. Например, два суждения: «Сократ высокий» и «Сократ низкий» (одно из них нечто утверждает, а другое то же самое отрицает, ведь высокий — это не низкий, и наоборот), — не могут быть одновременно истинными, если речь идёт об одном и том же Сократе, в одно и то же время его жизни и в одном и том же отношении, то есть, если Сократ по росту сравнивается не с разными людьми одновременно, а с одним человеком. Понятно, что когда речь идет о двух разных Сократах или об одном Сократе, но в разное время его жизни, например в 10 лет и в 20 лет, или один и тот же Сократ и в одно и то же время его жизни рассматривается в разных отношениях, например он сравнивается одновременно с высоким Платоном и низким Аристотелем, тогда два противоположных суждения вполне могут быть одновременно истинными, и закон противоречия при этом не нарушается. Символически он выражается следующей тождественно-истинной формулой: (а Λ а), (читается: «Неверно, что а и не а»), где а — это какое-либо высказывание. Закон исключённого третьего (лат. tertium non datur, то есть «третьего не дано») — закон классической логики, состоящий в том, что из двух высказываний — «А» или «не А» — одно обязательно является истинным, то есть два суждения, одно из которых является отрицанием другого, не могут быть одновременно ложными. Закон исключённого третьего является одним из основополагающих принципов «классической математики».С «интуиционистской» (и, в частности, «конструктивистской») точки зрения, установление истинности высказывания вида «А или не А» означает либо (а) установление истинности , либо (б) установление истинности его отрицания 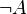. Поскольку, вообще говоря, не существует общего метода, позволяющего для любого высказывания за конечное число шагов установить его истинность или истинность его отрицания, закон исключённого третьего не должен применяться в рамках интуиционистского и конструктивного направлений в математике как аксиома.

10.Закон достаточного основания как выражение требования доказательности мышления. Сложности с его применением.

Наши мысли о каком-либо факте, явлении, событии могут быть истинными и ложными. Высказывая истинную мысль, мы должны обосновывать ее истинность, то есть доказать ее соответствие с действительностью.Требование доказательности мышления, обоснованности суждений выражает закон достаточного основания, который формулируется следующим образом: всякая истинная мысль имеет достаточное основание.Достаточным, то есть действительным, невымышленным основанием наших мыслей может являться личный опыт, индивидуальная практика. Истинность некоторых суждений подтверждается путем их непосредственного сопоставления с фактами действительности.Но личный опыт ограничен. Поэтому человеку в своей деятельности приходится опираться на опыт других людей.Благодаря развитию научных знаний человек все шире использует в качестве оснований своих мыслей предыдущий опыт всего человечества, закрепленный в законах и аксиомах науки, в принципах и положениях, существующих в любой области человеческой деятельности.Истинность законов, аксиом и т. д. подтверждена практикой человечества и не нуждается поэтому в новом подтверждении. Для подтверждения какого-либо частного случая нет необходимости обращаться к его практической проверке, обосновывать его при помощи личного опыта. Если, например, нам известен закон Архимеда (всякое тело, погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость), то нет никакой необходимости погружать в жидкость какой-либо предмет, чтобы выяснить, сколько он теряет в весе. Закон Архимеда будет достаточным основанием для подтверждения этого частного случая.Благодаря науке, которая в своих законах и принципах закрепляет всю общественно-историческую практику человечества, мы для обоснования наших мыслей не прибегаем всякий раз к их практической проверке, а обосновываем их теоретически, путем сопоставления с установленными уже ранее закономерностями.Таким образом, достаточным основанием какой либо мысли может быть любая другая, уже проверенная и признанная истинной мысль, из которой вытекает истинность другой мысли.Закон достаточного основания - общий логический принцип, согласно которому положение считается истинным только в том случае, если для него может быть сформулировано достаточное основание. Достаточное основание есть положение (или совокупность положений), которое является заведомо истинным и из которого логически вытекает обосновываемое положение. Истинность основания может быть или доказана опытным путем, на практике, или выведена из истинности др. положений. Закон достаточного основания характеризует одну из существенных черт логически правильного мышления - доказательность. Закон достаточного основания был впервые сформулирован Лейбницем, хотя он подразумевался и ранее во многих системах логики (напр., у Левкиппа, Аристотеля). По своему характеру закон достаточного основания является весьма общим методологическим принципом.Закон достаточного основания занимает важное место среди формально-логических законов мышления. Он тоже находится в неразрывной связи с остальными. И действительно, если мысль обладает определенностью (закон тождества), то это открывает возможность для установления ее истинности или ложности во взаимоотношениях с другими мыслями (закон противоречия и закон исключенного третьего). Само же установление истинности или ложности мысли невозможно без соответствующего обоснования.Отсюда - действие закона достаточного основания. Им обусловлена еще одна коренная черта правильного мышления наряду с определенностью и последовательностью, непротиворечивостью - его обоснованность, доказательность.Объективные предпосылки и смысл закона достаточного основания.Качественно определенные предметы, известным образом соотносящиеся между собой, так или иначе возникают из других предметов и сами, в свою очередь, порождают третьи, изменяются и развиваются в процессе взаимодействия между собой. Следовательно, все в окружающем мире имеет свои основания в другом. Такая объективно существующая универсальная зависимость одних предметов от других и служит важнейшей предпосылкой возникновения и функционирования в нашем мышлении закона достаточного основания. Этот закон был открыт и впервые сформулирован Г. Лейбницем. Он писал: «Ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым - без достаточного основания, почему именно дело обстоит так, а не иначе...»Правда, у Лейбница он дан как универсальный закон и бытия, и познания - закон причинности. Применительно лишь к мышлению ему можно дать следующую формулировку: ни одно суждение не может быть признано истинным без достаточного основания. Отсюда - название самого закона. Но почему идет речь именно о «достаточном» основании? Достаточными являются такие фактические и теоретические основания, из которых данное суждение следует с логической необходимостью.Примерная формула закона: «А истинно, потому что есть достаточное основание В».Логическое основание неразрывно связано с объективным, но в то же время и отлично от него. Объективным основанием служит причина, а результат ее действия - следствие. Логическим же основанием может выступать ссылка как на причину, так и на следствие. Классический пример. Дождь прошел. Это объективное основание (причина) того, что крыши домов мокрые (следствие), но не наоборот. Логических же оснований в рассуждении об этой причинно-следственной связи может быть два: «Крыши домов мокрые, потому что прошел дождь» и «Прошел дождь, потому что крыши домов мокрые». Почему это возможно? Потому что причина и следствие связаны между собой необходимым образом. Если есть причина, то есть и следствие, и наоборот: если есть следствие, то есть и причина. Надо только учитывать фактор «множественности причин» или «множественности следствий».Какова сфера действия закона достаточного основания? Если закон тождества явился обобщением прежде всего практики оперирования понятиями, а закон противоречия и исключенного третьего - практики функционирования суждений, то закон достаточного основания есть результат обобщения практики получения выводного знания. В нем выражено отношение одних истинные мыслей к другим - отношение логического следования, обеспечивающего в конечном счете их соответствие действительности. Этот закон означает, что в правильном рассуждении вывод всегда достаточно обоснован. Следовательно, в сферу действия этого закона входят прежде всего умозаключения. Когда, например, из двух посылок: «Все живое смертно» и «Люди - живые существа» мы делаем вывод, что «Все люди смертны», то это означает: «Все люди смертны» потому, что «Все живое смертно». Подведение того или иного предмета мысли под общее понятие служит достаточным основанием для распространения на него всех тех свойств, которые присущи всему классу предметов, мыслимому в этом понятии.В сфере действия закона достаточного основания находятся также доказательства. Уже само их существование есть показатель того, что такой закон существует. Кроме того, одно из важнейших правил доказательства - правило не только необходимости, но и достаточности оснований - прямо обусловлено действием этого закона. Например, существует объективная связь между ясным мышлением и ясным изложением. Поэтому если мы хотим обосновать, почему человек ясно излагает свои мысли, то можем сослаться на то, что он ясно мыслит. Это достаточное основание. Впрочем, можно сказать и наоборот: «Он ясно мыслит, потому что ясно излагает». Это тоже достаточное логическое основание.

Требования, вытекающие из закона достаточного основания, и ошибки, связанные с их нарушением. Будучи объективным, закон достаточного основания предъявляет к нашему мышлению важные требования: всякая истинная мысль должна быть обоснованной, или: нельзя признать высказывание истинным, если для него нет достаточных оснований. Иными словами, ничего нельзя принимать на веру: надо основываться на достоверных фактах и ранее доказанных положениях. Этот закон направлен против бессвязных, хаотичных, бездоказательных рассуждении; голого, необоснованного теоретизирования; неоправданных, неубедительных выводов. Он враг всяких догм, пустых верований, суеверий и предрассудков.Важнейшей логической ошибкой, связанной с нарушением требований закона достаточного основания, выступает «non sequitur» («не следует») - ошибка «мнимого следования». Она обнаруживается там, где нет достаточной логической связи между посылками и заключением, между тезисом и основаниями, доводами и выводами.Образцом подобной нелогичности служит рассуждение философов-лилипутов в произведении Джонатана Свифта «Путешествие Самюэля Гулливера»: «Вы утверждаете, правда, что на свете существуют другие королевства и государства, где живут такие же гиганты, как вы. Однако наши философы сильно сомневаются в этом... Ведь не подлежит никакому сомнению, что сто человек вашего роста могут за самое короткое время истребить все плоды и весь скот во владениях его величества. Кроме того, у нас есть летописи. Они заключают в себе описание событий за время в шесть тысяч лун, но ни разу не упоминают ни о каких других странах, кроме двух великих империй - Лилипутии и Блефуску». Здесь снова вывод не вяжется с доводами. Если в летописях нет упоминания о каком-либо событии, то это еще не значит, что его не было на самом деле. Существование события не связано необходимым образом с летописями.Или классический пример с Катюшей Масловой из романа Л. Толстого «Воскресение» В связи с убийством (отравлением) купца Смелькова Маслова была приговорена к каторжным работам и сделано это вследствие не только судебной, но и логической ошибки. Ею как раз и была ошибка под названием non sequitur («не следует»). Если бы в решении суда присяжных было записано: «Виновна, но без умысла ограбления и без намерения лишить жизни», Маслова была бы оправдана.

Ошибка «мнимого следования» иногда сознательно допускается для создания комичной ситуации, шутки и т. п. Мы находим, например, у бессмертного Козьмы Пруткова: «Я поэт, поэт даровитый! Я в этом убедился; убедился, читая других: если они поэты, так и я тоже». Или: «Смерть для того поставлена в конце жизни, чтобы удобнее к ней приготовиться».

Значение закона достаточного основания. Этот закон, разумеется, ничего не говорит о том, какие конкретно основания для данного вывода являются достаточными. Он только дисциплинирует наше мышление, направляя его на поиск таких оснований, на обеспечение обоснованности вывода. Это особенно важно в научном познании, прежде всего в теоретических науках, где велика роль выводного знания. Вот почему Г. Лейбниц придавал фундаментальное значение не только принципу противоречия, но и принципу достаточного основания. Он имеет большое значение, в частности, в связи с коренным вопросом теории познания - о критерии истинности наших знаний. Установлено, что таким критерием служит прежде всего общественная практика - материально-производственная, общественно-политическая деятельность, практика научных наблюдений и экспериментов. Именно она позволяет надежно отделять истинные знания от ложных. Однако далеко не все знания возможно и необходимо проверять непосредственно на практике. Если мы знаем, что существует закон всемирного тяготения, то нет надобности каждый раз проверять, упадет предмет или нет, когда мы его выпустим из рук. Это можно сделать и логическим путем: вывести одно знание из другого, уже проверенного на практике и получившего статус истинного. Следовательно, наряду с коренным, практическим критерием истинности наших знаний есть и другой - производный, логический критерий. Весь вопрос только в том, достаточны ли логические основания для того или иного вывода. На правильное решение этого вопроса и ориентирует нас закон достаточного основания.В практической деятельности тоже важно руководствоваться этим законом. Так, известный русский социолог Питирим Сорокин (с 1922 г. - в эмиграции), выступая против извращений в строительстве социализма в нашей стране, заявлял: «Можно и должно звать всех к производительной работе по возрождению страны, но ниоткуда не следует, что эта работа может и должна совершаться только по штампам и циркулярам в качестве агентов власти и чиновников, или обратно - должна быть непременно работой, низвергающей власть». Таким образом, автор отмечал известное отсутствие последовательности в определенных тогдашних практических действиях власти в стране. И позднее не было достаточных оснований для того, чтобы в экономике страны десятилетиями игнорировать мировой опыт развития рыночных отношений. Но и в настоящее время, когда произошла смена власти, многие ее действия представляются тоже недостаточно обоснованными, правда, уже в ином социальном смысле. Так, нередко опыт предшествующего развития страны огульно отрицается лишь на том основании, что он в конечном счете не удался. Однако это еще не достаточное основание для подобного нигилизма.Закон достаточного основания имеет прямое отношение к юридической практике. В законодательстве довольно широко распространено само понятие «достаточные основания». Так, в уголовном процессе по отношению к обвиняемому (а в исключительных случаях к подозреваемому) законом предусмотрены меры пресечения при наличии для этого достаточных оснований. Причем сами эти основания раскрываются.В гражданском законодательстве говорится, что гражданские права и обязанности возникают из предусмотренных законом оснований.В судебной практике дело может стать предметом судебного разбирательства, если для этого есть достаточные основания. Приговор или решение суда должны быть мотивированными, то есть обоснованными.В повседневной речи, говоря о том, что многие законы не действуют, мы приводим в качестве основания то, что нет процедуры их использования и т. д.Таким образом, закон достаточного основания имеет важное теоретическое и практическое значение. Фиксируя внимание на суждениях, обосновывающих истинность выдвинутых положений, этот закон помогает отделить истинное от ложного и прийти к верному выводу. Требование закона достаточного основания сводиться к тому, что всякое суждение, прежде чем быть принятым за истину, должно быть обоснованно. Обоснованность - важнейшее свойство логического мышления. Во всех случаях, когда мы утверждаем что-либо, убеждаем в чем-либо других, мы должны доказывать наши суждения, приводить достаточные основания, подтверждающие истинность наших мыслей.

11. Понятие как форма мысли. Языковые формы выражения понятий. Термины. Роль понятий в познании. Основные логически приемы формирования понятий.

Понятие - мысль, которая выделяет из некоторой предметной области и собирает в класс (обобщает) объекты посредством указания на их общий и отличительный признак. Напр., понятие "четырехугольник с равными сторонами и равными углами" выделяет множество квадратов из области четырехугольников на основе признака "иметь равные стороны и равные углы".Понятие (наряду с суждением и научной теорией) - одна из основных форм отражения мира на рациональной, логической ступени познания. Понятия представляют собой идеальные сущности, продукты мыслительной деятельности человека, их функция состоит в мысленном объединении разнородных объектов в единый класс и реализуется за счет выделения признака, присущего каждому из обобщаемых в понятии объектов и не присущего никакому другому объекту исходной предметной области, которая называется универсумом или родом понятия. Языковыми формами выражения понятия являются слова и словосочетания. Существуют слова-омонимы и слова-синонимы. Понятие – одна из основных форм научного познания.
Формируя понятие, наука отражает в них изучаемые ею предметы, явления, процессы. Например, экономическая теория сформировала такие понятия, как «товар», «капитал», «стоимость»; правовые науки – понятия «преступление», «наказание», «вина», «умысел», «правоспособность» и др. Логика (от греческого слова logos – «мысль», «слово», «разум», «закономерность») – наука о мышлении. Но в отличие от других наук, изучающих мышление человека, например физиологии высшей нервной деятельности или психологии, логика изучает мышление как средство познания. Одной из форм мышления является понятие. Понятия являются формой идеального отображения внешнего мира, т.е. объективной реальности в человеческом мышлении, и под правовым понятием понимают правовое значение или правовой смысл определённого выражения.Тема понятия является особенно актуальной в наши дни, так как, во-первых, постоянно появляются новые науки и, соответственно, новые термины. Во-вторых, человек, использующий в своей речи различные термины, должен четко их определять, чтобы иметь полное представление о том, что говорит он или другие. Управленческая деятельность подразумевает под собой четкую, понятную речь. Это возможно, если человек образован, грамотен. Применение понятий в мышлении необходимо всегда, когда к мышлению предъявляются требования определенности, точности и особенно доказательности. Специфика этой формы мышления состоит в том, что она, прежде всего, представляет собой результат мысленного, а значит и словесно-языкового выделения предметов некоторого класса.

12.Предметы и классы предметов, признаки класса. Круги Эйлера

Круги Эйлера Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783).Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля.Условно принято, что круг наглядно изображает объем одного какого-нибудь понятия. Объем же понятия отображает совокупность предметов того или иного класса предметов. Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга, как это показано на рисунке:

Группа предметов, составляющая вид данного класса предметов, изображается в виде меньшего круга, нарисованного внутри большего круга, как это сделано на рисунке.

Такое именно отношение существует между объемами понятий «небесное тело» (А) и «комета» (B). Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».В тех случаях, когда объемы двух понятий совпадают только частично, отношение между объемами таких понятий изображается посредством двух перекрещивающихся кругов, как это показано на рисунке:

Такое именно отношение существует между объемом понятий «учащийся» и «комсомолец». Некоторые (но не все) учащиеся являются комсомольцами; некоторые (но не все) комсомольцы являются учащимися. Незаштрихованная часть круга А отображает ту часть объема понятия «учащийся», которая не совпадает с объемом понятия «комсомолец»; незаштрихованная часть круга B отображает ту часть объема понятия «комсомолец», которая не совпадает с объемом понятия «учащийся». 3аштрихованиая часть, являющаяся общей для обоих кругов, обозначает учащихся, являющихся комсомольцами, и комсомольцев, являющихся учащимися.\Когда же ни один предмет, отображенный в объеме понятия A, не может одновременно отображаться в объеме понятия B, то в таком случае отношение между объемами понятий изображается посредством двух кругов, нарисованных один вне другого. Ни одна точка, лежащая на поверхности одного круга, не может оказаться на поверхности другого круга.

Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.Отношения между равнозначащими понятиями, объемы которых совпадают, отображаются наглядно посредством одного круга, на поверхности которого написаны две буквы, обозначающие два понятия, имеющие один и тот же объем:

Такое отношение существует, например, между понятиями «родоначальник английского материализма» и «автор „Нового Органона“». Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.Нередко бывает и так: одному понятию (родовому) подчиняется сразу несколько видовых понятий, которые в таком случае называются соподчиненными. Отношение между такими понятиями изображается наглядно посредством одного большого круга и нескольких кругов меньшего размера, которые нарисованы на поверхности большего круга:

Такое именно отношение существует между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия в равной мере подчинены одному общему родовому понятию «музыкальные инструменты».Круги, изображающие соподчиненные понятия, не должны касаться друг друга и перекрещиваться, так как объемы соподчиненных понятий несовместимы; в содержании соподчиненных понятий имеются, наряду с общими, различающие признаки. Эта схема отображает общее, что характерно для отношения любых соподчиненных понятий, взятых из различных областей знания. Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.

В тех случаях, когда между понятиями имеется отношение противоположности, отношение между объемами таких понятий отображается посредством одного круга, обозначающего общее для обоих противоположных понятий родовое понятие, а отношение между противоположными понятиями обозначается так: А — родовое понятие, B и C — противоположные понятия. Противоположные понятия исключают друг друга, но входят в один и тот же род, что можно выразить такой схемой:

При этом видно, что между противоположными понятиями возможно третье, среднее, так как они не исчерпывают полностью объема родового понятия. Такое именно отношение существует между понятиями «легкий» и «тяжелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и легкий, и тяжелый. Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.Когда же между понятиями существует противоречащее отношение, тогда отношение между объемами понятий изображается иначе: круг делится на две части так: А — родовое понятие, B и не-B (обозначается как B) — противоречащие понятия. Противоречащие понятия, исключают друг друга и входят в один и тот же род, что можно выразить такой схемой:

При этом видно, что между противоречащими понятиями третье, среднее, невозможно, так как они полностью исчерпывают объем родового понятия. Такое отношение существует, например, между понятиями «белый» и «не-белый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и белый и не-белый.Посредством эйлеровых кругов изображаются также отношения между объемами субъекта и предиката в суждениях. Так, в общеутвердительном суждении, выражающем определение какого-либо понятия, объемы субъекта и предиката, как известно, равны. Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке:

Иначе выглядит схема отношения между объемами субъекта и предиката в общеутвердительном суждении, не являющемся определением понятия. В таком суждении объем предиката больше объема субъекта, объем субъекта целиком входит в объем предиката. Поэтому отношение между ними изображается посредством большого и малого кругов, как показано на рисунке:

Примером первого вида отношений между объемами субъекта и предиката может служить суждение: «Все квадраты — равносторонние прямоугольники»; примером второго вида отношений между объемами предиката и субъекта может служить суждение: «Все квадраты — геометрические фигуры».Эйлеровы круги применяются также и для наглядного изображения отношений между терминами силлогизма. Например, силлогизм

4. Всякое A есть B;

5. Некоторые C есть A; Некоторое С есть В

Выражен им в виде такой схемы:

Тот факт, что какая-то часть пространства В включается в пространство С, Эйлер выражал звездочкой, как это показано на следующей схеме

Диаграммы Эйлера своим наглядным графическим изображением не только облегчают запоминание структуры различных сочетаний мыслей, но и помогают решению ряда задач, стоящих перед формальной логикой.Давно известно, что с помощью эйлеровых кругов легко можно проверить истинность, например, того или иного вида непосредственного умозаключения. Для этого надо сравнить условие (антецедент) и следствие (консеквент) данного непосредственного умозаключения с диаграммами Эйлера. Правило сравнения гласит: если какая-либо из диаграмм, отвечающих условию (антецеденту), не совпадает ни с одной из диаграмм, отвечающих заключению, то этот вид непосредственного умозаключения является ложным.Теперь допустим необходимо решить: истинно или ложно такое, например, непосредственное умозаключение: «Все S суть Р, следовательно, некоторые Р суть S».Поскольку условием в этом непосредственном умозаключении является общеутвердительное суждение, то его обозначают латинской буквой А (от affirmance), а все суждение кратко записать так: Asp; следствием в этом непосредственном умозаключении является частноутвердительное суждение, которое обозначается латинской буквой I, а все суждение кратко записать так: Ips. Теперь данное непосредственное умозаключение будет выглядеть так:Asp Ips.где — знак импликации, сходный с союзом «если …. то … ».После этого обратимся к диаграммам Эйлера, в которых отражены структуры всех категорических суждений относительно непустых множеств. Такими диаграммами могут быть пять следующих диаграмм:

Содержание и объем понятия. Закон обратного отношения содержания и объема понятия.

Объём понятия(в логике) — совокупность предметов, охватываемых понятием.Например, объём понятия «параллелограмм» включает множество всех возможных параллелограммов.

Содержание понятия — это совокупность существенных и отличительных признаков предмета, качества или множества однородных предметов, отражённых в этом понятии, поскольку с точки зрения логики всякое понятие имеет содержание и объём. Например, содержанием понятия «коррупция» является совокупность двух существенных признаков: «сращение государственных структур со структурой преступного мира» и «подкуп и продажность общественных и политических деятелей, государственных чиновников и должностных лиц».

Закон обратного отношения между объёмом и содержанием понятия — закон формальной логики о зависимости между изменениями объёма и содержания понятия[1]. Если первое понятие шире второго по объёму, то оно беднее его по содержанию; если же первое понятие у́же второго по объему, то оно богаче его по содержанию. Например, понятие «физика» обладает ме́ньшим объёмом, чем понятие «наука». При этом содержание понятия «физика» больше (богаче), чем содержание понятия «наука», так как помимо своих собственных содержит все признаки понятия «наука». Закон применим только при вхождении объёма одного понятия в объём другого, например: «животное» — «собака». Закон не работает для несовпадающих понятий, например: «книга» — «кукла».Уменьшение объёма понятия с добавлением новых признаков (то есть, расширением содержания) наступает не всегда, а только когда признак свойственен части объёма исходного понятия.