
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отношения между понятиями. По содержанию между понятиями могут быть только два вида отношений – сравнимость и несравнимость
По содержанию между понятиями могут быть только два вида отношений – сравнимость и несравнимость. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (романс и кирпич). Между ними невозможны логические отношения.Сравнимые понятия – это понятия, имеющие в своем содержании общие, существенные признаки (по которым они и сравниваются). Напр., право и мораль. Отношения между понятиями изображают с помощью схем – кругов Эйлера. Между сравнимыми понятиями возможны два вида отношений по объему: совместимость и несовместимость.Совместимые понятия – это такие, объемы которых полностью или частично совпадают. Между совместимыми понятиями складываются следующие отношения:1 – равнообъемность. Равнообъемными или равнозначными называются понятия, которые различаются по своему содержанию, но объемы которых совпадают. Напр., «Л.Н. Толстой» – А и «автор романа «Война и мир» – В. Объемы тождественных понятий изображаются кругами, полностью совпадающими.
2 – перекрещивание. Перекрещивающимися называются понятия, объемы которых частично совпадают, напр. «студент» и «спортсмен», «юрист» и «писатель». Они изображаются пересекающимися кругами. В перекрещивающейся части двух кругов мыслятся студенты, являющиеся спортсменами. В левой части круга мыслятся студенты, не являющиеся спортсменами, а в правой части – спортсмены, не являющиеся студентами.
3 – подчинение. В отношении подчинения (субординации) находятся понятия, если объем одного полностью входит в объем другого, но не исчерпывает его. Это отношение вида – В и рода – А (млекопитающее и кошка).
Несовместимыми называются понятия, объемы которых не совпадают. Несовместимые понятия могут находиться между собой в следующих отношениях.1 – соподчинение. В отношении соподчинения (координации) находятся понятия, объемы которых исключают друг друга, но принадлежат некоторому более общему родовому понятию. Напр., «ель» – B, «береза» – C принадлежат объему понятия «дерево» – А. Они изображаются неперекрещивающимися кругами внутри общего круга. Это виды одного и того же рода.
2 – противоположность. В отношении противоположности (контрарности) находятся два понятия, признаки которых противоречат друг другу, а сумма их объемов не исчерпывает родового понятия (храбрость – трусость).
3 – противоречие. В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя никакими другими (напр., А – белая краска, тогда понятие, находящееся с ним в отношениях противоречия, следует обозначить не-А (не белая краска). Круг Эйлера в этом случае делится пополам и между ними нет никакого третьего понятия.
16.Операции с классами предметов: пересечение, объединение, дополнение, разность. Диаграммы Венна.
. С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множествОбъединением А 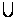 В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.Символическая запись этого определения: А
В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.Символическая запись этого определения: А 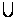 В={х | х
В={х | х  А или х
А или х  В}. Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз). Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
В}. Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз). Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
 На диаграмме объединение множеств А и В выделено штриховкой.Если множество А определяется характеристическим свойством Р (х), а множество В - характеристическим свойством Q(х), то А
На диаграмме объединение множеств А и В выделено штриховкой.Если множество А определяется характеристическим свойством Р (х), а множество В - характеристическим свойством Q(х), то А 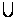 В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А 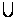 В ={2; 3; 5; 6; 7}.2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А
В ={2; 3; 5; 6; 7}.2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А 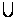 В=[-2/3; 2] .3) Пусть А= {х | х=8k, k
В=[-2/3; 2] .3) Пусть А= {х | х=8k, k  Z}, B={x | x=8n-4, n
Z}, B={x | x=8n-4, n  Z}. Тогда A
Z}. Тогда A 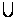 B ={x | 4m, m
B ={x | 4m, m  Z}.Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств. Объединением системы множеств {Аα} называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются. Таким образом, элемент х
Z}.Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств. Объединением системы множеств {Аα} называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются. Таким образом, элемент х  тогда и только тогда, когда найдется такой индекс α 0
тогда и только тогда, когда найдется такой индекс α 0  М, что х
М, что х  A α0 . В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись
A α0 . В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись  Если M=N, то имеем объединение последовательности множеств
Если M=N, то имеем объединение последовательности множеств  .Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда
.Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда  = [0;2). Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1
= [0;2). Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1 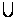 A2 = A2
A2 = A2 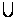 А1, и ассоциативна, т.е. (А1
А1, и ассоциативна, т.е. (А1 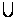 A2)
A2) 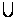 А3 = А1
А3 = А1 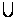 (A2
(A2 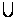 А3).
А3).
16..
17..Пересечение множеств .Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.Символическая запись этого определения: А ∩ В={х | х  А и х
А и х  В}.Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
В}.Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
 А ∩ В.На диаграмме пересечение множеств А и В выделено штриховкой.Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х).Примеры пересечений двух множеств:Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩ В={5; 7}.Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m
А ∩ В.На диаграмме пересечение множеств А и В выделено штриховкой.Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х).Примеры пересечений двух множеств:Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩ В={5; 7}.Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m  Z}.Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов. Операцию пересечения можно определить и для произвольной системы множеств {Аα}, где α
Z}.Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов. Операцию пересечения можно определить и для произвольной системы множеств {Аα}, где α  М. Пересечением системы множеств {Аα}, называется множество
М. Пересечением системы множеств {Аα}, называется множество  , состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α
, состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α  М, т.е.
М, т.е.  = {x | x
= {x | x  Аα для каждого α
Аα для каждого α  М}.
М}.
В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись 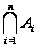 . Если M=N, то имеем пересечение последовательности множеств
. Если M=N, то имеем пересечение последовательности множеств  .
.
В рассмотренном выше примере системы множеств Аα =[0; α], α  М =(1; 2) получим:
М =(1; 2) получим:  =[0;1]. Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1∩A2 = A2 ∩А1 и (А1∩A2)∩ А3= А1∩(A2 ∩ А3).
=[0;1]. Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1∩A2 = A2 ∩А1 и (А1∩A2)∩ А3= А1∩(A2 ∩ А3).
Разность множествРазностью АВ множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.АВ={х | х  А и х
А и х  В},что можно пояснить на диаграмме Эйлера-Венна следующим образом:
В},что можно пояснить на диаграмме Эйлера-Венна следующим образом:
 На диаграмме разность АВ выделена штриховкой.Примеры разностей множеств:Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда АВ ={2;7}, а ВА={3; 6}.Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда АВ=(7/4;2], а ВА=[-2/3; -1/4).Пусть А - множество всех четных целых чисел, В - множество всех целых чисел, делящихся на 3. тогда АВ - множество всех четных целых чисел, которые не делятся на 3, а ВА –множество всех нечетных целых чисел, кратных трем.
На диаграмме разность АВ выделена штриховкой.Примеры разностей множеств:Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда АВ ={2;7}, а ВА={3; 6}.Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда АВ=(7/4;2], а ВА=[-2/3; -1/4).Пусть А - множество всех четных целых чисел, В - множество всех целых чисел, делящихся на 3. тогда АВ - множество всех четных целых чисел, которые не делятся на 3, а ВА –множество всех нечетных целых чисел, кратных трем.
Дополнение множестваПусть множество А и В таковы, что А 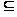 В. Тогда дополнением множества А до множества В называется разность ВА. В этом случае применяется обозначение СBА=ВА. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=UА и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:
В. Тогда дополнением множества А до множества В называется разность ВА. В этом случае применяется обозначение СBА=ВА. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=UА и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:  СА={x | x
СА={x | x  A}. На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА:
A}. На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА:


Дата добавления: 2015-01-19; просмотров: 308; Мы поможем в написании вашей работы!; Нарушение авторских прав |