Барометрическая формула. Распределение Больцмана. Распределение Максвелла - Больцмана.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид: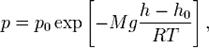

где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону: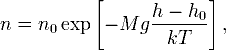

где M — молярная масса газа, k — постоянная Больцмана.

Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот Δh между двумя точками по измеряемому в этих точках давлению (p₁ и p₂). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга