Неравенство Клаузиуса. Равенство Клаузиуса. Энтропия. Изэнтропический процесс. Теорема Нернста(третье начало термодинамики).

Энтропия изолированной системы не может убывать. dS≥0 (Неравенство Клаузиуса)

В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство переходит в Равенство Клаузиуса: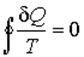

Энтропия системы — функция её состояния, определённая с точностью до произвольной постоянной, разность которых в двух равновесных состояниях 1 и 2 по определению равна приведённому количеству теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути.

Закон возрастания энтропии. Энтропия адиабатически изолированной системы либо возрастает, либо остаётся постоянной.

Термин широко применяется и в других областях знания: в статистической физике — как мера вероятности осуществления какого-либо макроскопического состояния

Изоэнтропийный процесс - тепловой процесс, происходящий при постоянной энтропии.

Условия, при которых тепловой процесс будет изоэнтропийным, можно получить из равенства Клаузиуса для обратимых процессов: ,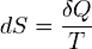

где dS - приращение (дифференциал) энтропии, а δQ - бесконечно малое полученное количество теплоты. Отсюда следует, что из обратимых процессов изоэнтропийным является только обратимый адиабатный процесс.

Из неравенства Клаузиуса для необратимых процессов ,

следует, что необратимый адиабатный процесс не может быть изоэнтропийным.

Но вообще и при необратимом процессе энтропия системы может сохранять постоянное значение, если вся производимая энтропия сразу удаляется с помощью теплообмена.

Линию на любой термодинамической диаграмме, изображающую изоэнтропийный процесс, можно называть изоэнтропой. Но обычно её называют адиабатой, так как необратимый процесс (в том числее необратимый адиабатный) нельзя корректно изобразить линией на диаграмме.

Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при абсолютном нуле температуры. Является одним из постулатов термодинамики.

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

или

где x — любой термодинамический параметр.

третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):

третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.