Интерференция. Сложение в пространстве волн, при котором образуется постоянное но времени распределение амплитуд результирующих колебаний частиц среды, называетсяинтерференцией1.

Выясним, при каких условиях наблюдается интерференция волн. Для этого рассмотрим более подробно сложение волн, образующихся на поверхности воды.

Можно одновременно возбудить две круговые волны в ванне с помощью двух птариков, укрепленных на стержне, которые совершают гармонические колебания (рис. 8.43). В любой точке М на поверхности воды (рис. 8.44) будут складываться колебания, вызванные двумя волнами (от источников O₁ и О₂). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, различаться, так как волны проходят различные пути d₁ и d₂. Но если расстояние I между источниками много меньше этих путей 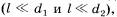то обе амплитуды можно считать практически одинаковыми.

Результат сложения волн, приходящих в точку М, зависит от разности фаз между ними. Пройдя различные расстояния d₁ и d₂ волны имеют разность хода

d = d₂ - d₁. Если разность хода равна длине волны , то вторая волна запаздывает по сравнению с первой на один период (именно за период волна проходит путь, равный ее длине волны ). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.

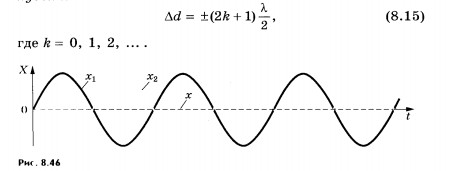
Условие максимумов. На рисунке 8.45 изображена зависимость от времени смещений х₁и х₂ волнами при d = . Разность фаз колебаний равна нулю (или, что то же самое, 2 так как период синуса равен 2 ). В результате сложения этих колебаний возникают результирующие колебания с удвоенной амплитудой. Колебания результирующего смещения х на рисунке показаны цветной штриховой линией.

¹ От латинских слов inter — взаимно, между собой и ferio ударяю, поражаю.

То же самое будет происходить, если на отрезке d укладывается не одна, а любое целое число длин волн.

Амплитуда колебаний частиц среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:



где k = 0, 1, 2, ... .

Условие минимумов. Пусть теперь на отрезке Ad укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной л, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующих колебаний равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 8.46). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.

Амплитуда колебаний частиц среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:



Если разность хода d₂ - d₁ принимает промежуточное значение между то и амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важно то, что амплитуда колебаний в любой точке не меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 8.47 показана фотография интерференционной картины для двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.

Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебанийбыла постоянной.

Источники, соответствующие этим двум условиям, называются когерентными¹.Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина.

Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться с течением времени. Поэтому амплитуда результирующих колебаний с течением времени будет непрерывно изменяться. В результате максимумы и минимумы перемещаются в про странстве, и интерференционная картина размывается.

Распределение энергии при интерференции. Волны несут энергию. Что же с этой энергией происходит при гашении волн друг другом? Может быть, она превращается в другие формы, и в минимумах интерференционной картины выделяется тепло? Ничего подобного!

Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем. Вследствие интерференции происходит пepepaспредилениe энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает вовсе.

¹От латинского слова cohaereus — влаимосвязанный.

Обнаружение интерференционной картины доказывает, что мы наблюдаем волновой процесс. Волны могут гасить друг друга, а сталкивающиеся частицы никогда не уничтожают друг друга целиком. Интерферируют только когерентные (согласованные) волны.

50!!!!!!!!!!!!!!!!!!!!!!!!! Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам) , определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли) , а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл) . Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках) , зато это можно делать на частотах, равных долям от основной (низших гармониках). Резонансные явления могут вызвать необратимые разрушения в различных механических системах. В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения. Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов. Струна Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов) . Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:

Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка) , струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты) . Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты