Односторонние функции

Односторонняя (one-way) функция — это функция, которую просто вычислять, но трудно обращать. Пример — умножение больших чисел. Мы можем вычислить без слишком больших трудностей произведение:

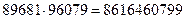
но обратный процесс — факторизация (разложение на множители) числа 8 616 460 799 существенно труднее. В.С. Джевонс (W.S. Jevons), рассматривавший эту проблему в 1873 г., резю­мировал, что "мы можем легко... сделать некоторую вещь, но можем иметь много неприятностей, если попытаемся разделить ее".

В качестве операции факторизации для системы с общим ключом нам бы хо­телось иметь такую функцию, которая при работе на сообщении давала бы в результате криптограмму 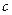, по которой практически невозможно раскрыть . Другими словами, мы должны быть способны легко выполнять функцию 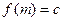(так, чтобы криптосистема оставалась реализуемой), но реализовать 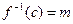было бы практически невозможно. Заметим, что обращение функ­ции теоретически всегда возможно (скажем, просто путем вычисления 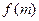для каждого возможного сообщения до тех пор, пока результат не совпадет с 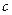). Однако стоимость выполнения таких вычислений была бы значительно выше, чем значимость информации, которая могла быть получена таким спо­собом, или время, затраченное на это было бы так велико, что полученная информация оказалась бы устаревшей.

Односторонние функции, используемые для криптографических целей, должны обладать еще одним свойством — они должны иметь специальную "лазейку", т.е. способ, с помощью которого некто, обладающий специальным знанием, смог бы восстановить по 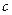, затратив разумное количество усилий. Это секретное знание формирует частный ключ, который тайно хранится получателем, позволяя ему расшифровывать сообщения.

Система работает следующим образом.

1. Каждый пользователь имеет пару ключей и .
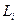2. Сообщение шифруется с помощью функции .
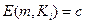3. Выполняется дешифрация с помощью функции .
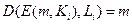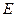4. и 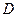проектируются так, чтобы:

а. для заданных и , можно было легко находить ;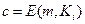

б. для заданного 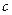было бы нереально найти (то есть функция 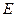должна быть односторонней);

в. для заданных 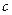и 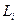, можно было легко найти (то есть функция 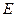должна иметь "лазейку", задаваемую параметром ).

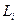Для использования в криптосистемах были предложены различные функции.

1. Ключевой обмен Диффи-Хеллмана (Diffie-Hellman). Основан на трудности вычисления дискретных логарифмов полей, которая возрастает по сравнению с вычислениями на основе степенных функций. Это не совсем шифр, но это первая опубликованная система с общим ключом.

2. RSA (криптосистема Райвеста, Шамира, Альдемана). Основана на трудности факторизации (разбиения на множители) произведения по сравнению с операцией умножения. Это наиболее популярная система с общим ключом, используемая, например, для почтовой программы, реали­зующей протокол POP (Post Office Protocol). Но в вычислительном отно­шении она довольно дорогая, и коммерческое ее использование в США подлежит патентованию.

3. Knapsack. Методика с таким странным названием основана на трудности разделения суммы на индивидуальные элементы по сравнению с добавлением этих элементов в начало суммы. Было много успешных атак на эту систему и в результате она используется довольно редко. Однако, она ме­нее сложна, чем RSA, и до появления более современных систем с эллиптическими кривыми ее считали системой, вполне оправдывающей свои обещания, т.е. обладающей низкой сложностью и относительной безопасностью.

4. Эллиптические кривые. Эллиптические кривые — это специальные ли­нии, определенные над первичным полем. Задав некоторую точку на этой линии, легче вычислять и все другие ее точки. Без генерации всех возмож­ных точек (что не практично, если поле достаточно велико) обращение операции довольно затруднительно. Эти схемы являются довольно много­обещающими, потому что кодирование и декодирование в них не очень-то сложное. Если не касаться защиты, то эта схема обладает всеми преиму­ществами предыдущей.

5. Коды с исправлением ошибок. Хотя код с исправлением ошибок способен исправлять до (d - l)/2 ошибок, но без набора декоди­рующих правил единственный способ реализовать эту возможность со­стоит в том, чтобы сравнивать полученный вектор с каждым кодовым сло­вом и выбирать тот, который находится на расстоянии (d- l)/2 от него. Для длинных кодов это практически невозможно. Поэтому можно сформировать криптосистему, использующую код с исправлением ошибок, выполняя перестановки генерирующей матрицы. Исходный генератор формирует частный ключ, позволяющий декодировать сообщения, а гене­ратор с перестановками используется в качестве общего ключа. Посылае­мые сообщения маскируются добавлением ошибок, которые подслуши­вающий не может удалить, т.к. генератор с перестановками не позволяет выполнить простое декодирование.