Ключевой обмен Диффи-Хеллмана

Протокол обмена ключей Диффи-Хеллмана в действительности не является обычной системой с общим ключом, т.к. передаваемый секрет случаен, но его можно использовать для передачи информации, применяя общий секрет для шифрования передаваемых данных. Это была первая опубликованная система с общим ключом. В ней возникают трудности, связанные с вычисле­ниями логарифмов первичных полей, которые значительно выше, чем при вычислениях с помощью экспоненциальных функций.

Протокол выполняет обмен секретом между двумя сторонами по опасному каналу, не требуя ни знания, ни даже существования этого секрета. Работает это следующим образом.

1. Алиса и Боб соглашаются использовать генератор 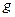и простой модуль .
2. Алиса генерирует случайное число 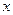. Это ее частный ключ. Она вычисля­ет свой общий ключ 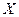, который равен .
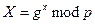3. Подобным же образом Боб генерирует случайный частный ключ 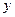и общий ключ 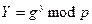. Алиса и Боб обмениваются их общими ключами 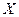и .
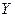4. Алиса принимает ключ 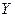и использует свой частный ключ 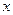для следую­щего вычисления: .
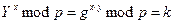5. Боб также может вычислить 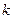по ключу 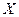, который он принимает от Али­сы, и своему частному ключу 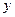, т.к. .
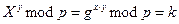6. И Алиса и Боб теперь знают 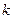, но подслушивающий не может вычислять 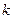по наблюдениям и .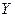

В качестве примера такого обмена рассмотрим следующую процедуру:

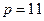1. и .
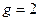2. Алиса получает случайный 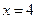, Боб выбирает .
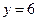3. Алиса вычисляет .
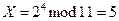4. Боб вычисляет .
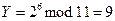5. Алиса посылает Бобу число 5, а Боб посылает Алисе число 9.
6. Алиса вычисляет .
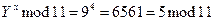7. Боб вычисляет .
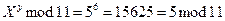8. Поэтому .

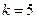Обратите внимание, что общий секрет случаен, т.к. 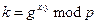, так что его нельзя использовать, чтобы напрямую посылать информацию. Если Алиса и Боб не выбирают свои частные ключи чисто случайно, то это знание можно использовать для нападения на систему.

Когда и 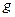опубликованы, то нападение на эту систему становится эффек­тивным с помощью задачи дискретного логарифмирования. 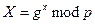оз­начает, что 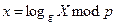. Поэтому Ева может находить 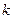, вычисляя 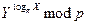. В вышеупомянутом примере нахождение 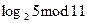триви­ально, но очень трудно, если велико.