Основные характеристики(вероятностные оценки погрешности).

соответствует определению среднего (2.2.3) только при . Таким образом, даже для оценки точности вычисления средней величины 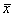необходимо учитывать форму статистического распределения исходных данных.

Статистические распределения принято оценивать по значениям их моментов. Моменты случайных величин, найденные без исключения систематических составляющих, называются начальными, а моменты для центрированных распределений —центральными.

Центральный момент -го порядка для непрерывной случайной величины рассчитывается по формуле

, (2.2.5)

при этом - математическое ожидание; - дисперсия (для конечной выборки — среднеквадратичное отклонение (СКО)); 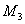характеризует асимметрию распределения, а безразмерный коэффициент асимметрии есть третий центральный момент, поделенный на СКО; 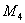характеризует протяженность распределения, отношение - эксцесс, -характеризует остроту вершины распределения.

Наиболее широкое распространение при обработке экспериментальных данных получил центральный момент второго порядка 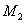который повсеместно используют для оценки погрешностей измерений. Для конечной выборки (конкретного числа отсчетов ) СКО принято рассчитывать по следующей формуле:

. (2.2.6)

Эта формула, как и формула (2.2.4) для вычисления 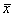, не учитывает форму распределения и не является строгой. Ее широкое использование обусловлено двумя основными причинами:

1. Это наиболее простая возможность оценить рассеяние случайной величины.

2. Значения случайных величин при экспериментальных измерениях имеют статистическое распределение, близкое к нормальному (гауссову), а для этого распределения среднеквадратичное отклонение и квадрат дисперсии совпадают.

Оценку асимметрии и эксцесса при конечной выборке осуществляют по следующим формулам

, (2.2.7)

. (2.2.8)

Число 3 в формуле (2.2.8) определяет эксцесс нормального распределения. Если эксцесс распределения отрицательный, то вершина функции распределения острее, чем у нормального распределения.

Определение этих характеристик распределений (моментов) называется точечными оценками, которые характеризуют распределение достаточно грубо.

Пусть в процессе экспериментальных измерений регистрируется сразу несколько случайных величин , каждая из которых имеет свое среднее значение и дисперсию . Многомерная случайная величина 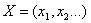будет иметь многомерное распределение вероятностей 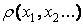с условием нормировки

.

Величины считаются статистически независимыми, если . Но эти величины могут быть статистически связаны, и для численной оценки этой связи двух случайных величин принято использовать смешанный момент второго порядка который называют корреляционным моментом или ковариацией.

Для расчета корреляционного момента используется следующая формула:

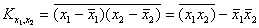, (2.2.9)

где черта сверху означает статистическое усреднение соответствующего выражения. Корреляционный момент есть смешанная дисперсия двух величин, поэтому для расчета коэффициента корреляции используется нормировка на дисперсию каждой из случайных величин:

. (2.2.10)

Коэффициент корреляции меняется в пределах от -1 до +1 и определяет степень связи случайных величин.

, (2.2.11)

а дисперсия их суммы .

Таким образом, складывать СКО необходимо с учетом того, насколько случайные погрешности коррелированы.

Если:

1) , то ;

2) , то .

Как правило, при сложении погрешностей их делят на две группы: коррелированные и некоррелированные. Разделение на большее число групп (некоррелированные, слабо коррелированные, сильно коррелированные) слишком трудоемко. Поэтому на практике коррелированными погрешностями считаются те, у которых , остальные — некоррелированные.

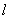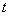Рассмотрим пример коррелированных погрешностей. Пусть измеряется зависимость активного сопротивления металлического проводника (длина , площадь сечения ) от температуры . Полученная экспериментально зависимость используется для проверки известной зависимости удельного сопротивления металлов от температуры

. (2.2.12)

Для вычисления по экспериментальным данным приходится использовать размеры проводника: . Но размеры проводника, также как и его удельное сопротивление, зависят от температуры по законам теплового расширения. На построение зависимости (2.2.12) будут влиять погрешности измерения , но погрешности в измерении при разных значениях температуры неизбежно будут связаны (коррелированы).