Погрешности косвенных измерений

В большинстве экспериментов используют косвенные измерения. Исследуемую величину f определяют по результатам прямых измерений других физических величин, например, x,y,z,...,с которыми она связана заранее установленным функциональным математическим соотношением

f = f(x, y, z, …) . (5.1)

Эта связь должна быть известна экспериментатору. Помимо данных прямых измерений, параметрами (5.1) могут оказаться другие величины, точно заданные или полученные в других измерениях, – они составляют набор исходных данных. Выражение (5.1), записанное в явном виде, называют рабочей формулой и используют как для оценивания результата косвенного измерения , так и для оценивания погрешности измерения f. Естественно, обе оценки связаны с окончательными результатами прямых измерений 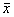±x, ±y, ± z, …… . Обычно, чтобы получить (5.1), используют модельное описание и, во избежание модельных погрешностей при измерении f, оно должно адекватно отражать исследуемое физическое явление. Если модель точна, то модельные погрешности исключены, а косвенное измерение дает надежные результаты.

Как и в предыдущем разделе, рассмотрим случай, когда погрешности измерения величин x, y, z, … носят только случайный характер и соответствуют нормальному закону распределения. Кроме этого, погрешность каждого отдельно взятого прямого измерения независима, т.е. не подвержена воздействию случайных факторов, вызывающих погрешности других прямых измерений, выполненных в эксперименте. Такие измерения и сами измеряемые величины носят название статистически независимых, или просто независимых. При выполнении указанных условий среднее значение величины f определяют на основе (5.1), исходя из средних значений величин x, y, z, … :

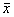= f( , , , …..) . (5.2)

Если точность прямых измерений достаточно высока, т.е. x<< 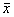, y<< ,  z<< , ... , то погрешности результатов прямых измерений переносятся на результат косвенного измерения как независимые нормальные распределения f вокруг по каждому из аргументов функции (5.1). Строгое обоснование этого утверждения можно найти в математической статистике. Погрешность измерения f вследствие малых случайных вариаций

только величины x: f_x=f_x'x ,

только величины y: f_y=f_y'y, (5.3)

только величины z: f_z=f_z'z, и т.д.

Здесь f_x', f_y', f_z'…..– производные функции f(x,y,z,…)по соответствующим переменным, являющиеся частными производными и обозначаемые в виде

f_x'= 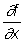, f_y'= 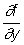, f_z'= , …… .

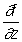Аргументами в вычисленных производных (5.3) служат оценки средних значений , , …. .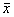

Совместное распределение f вокруг , которое учитывает отдельные распределения по каждому из аргументов (5.1), должно определять погрешность косвенного измерения  f. Эти распределения нормальны и независимы, поэтому дисперсия их совместного распределения равна сумме их дисперсий, что строго доказано в математической статистике. Тогда среднее квадратичное отклонение совместного распределения, вычисляемое как корень из дисперсии, следует находить из выражения:

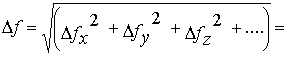
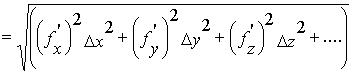. (5.4)

Это выражение имеет общий характер и его можно использовать для оценивания погрешности косвенного измерения, выполненного при любом виде функции f(x,y,z,…). Однако следует твердо помнить, что при непосредственных расчетах в (5.4) необходимо подставлять погрешности x, y, z …., найденные для одного и того же значения доверительной вероятности. Погрешность косвенного измерения также будет соответствовать этому значению доверительной вероятности. Рекомендуется использовать значение вероятности = 0,68. Применим (5.4) к некоторым распространенным зависимостям. Интерес представляют те случаи, когда с помощью (5.4) удается установить функциональную связь между погрешностями прямых измерений и погрешностью косвенного измерения. Таблица 5.1 содержит выражения, задающие такую связь.

Таблица 5.1. Связь погрешностей прямых и косвенных измерений.

Рабочая формула	Формула погрешности

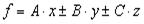
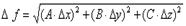
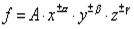
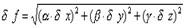
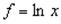
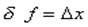
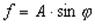
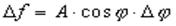
В таблице приняты следующие обозначения:  – для абсолютной погрешности,  – для относительной погрешности, A, B, C, – постоянные, x, y, z,  – результаты прямых измерений, f – результат косвенного измерения.

В качестве примера к рассмотренному материалу проведем обработку результатов эксперимента по измерению ускорения свободного падения g. В нем выполнено многократное прямое измерение времени падения t стального шарика с высоты h (двенадцатый этаж высотного дома), которая также определена многократным прямым измерением (см. пример предыдущего раздела). Экспериментальные результаты:

t = (2,43±0,11) c , h =(28,85±0,20) м .

Рабочая формула для определения g имеет вид g = .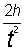

Согласно (5.2)

= 9,77 м/с2 .

Поскольку производные вычисляются как

g’_h = 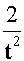, g’_t = , то согласно (5.4)

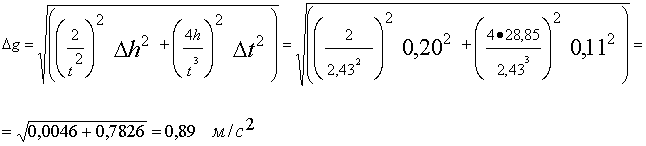
Чтобы не выполнять вычисление производных g’_h и g’_t , погрешность g можно найти с помощью второй строки табл.5.1, так как рабочая формула может быть записана в виде g=2ht^-2 .

Тогда

g²=h²+4t²=(0,0069)²+4(0,0453)²=0,0083

g= 0,091,

g=gg=9,77*0,091=0,89 м/с2 .

После округления окончательный результат косвенного измерения в стандартной форме:

g = (9,8 ± 0,9) м/с2 .

Из анализа погрешностей эксперимента видно, что основной вклад в g дает t. Поэтому повышение точности измерения ускорения свободного падения возможно только после увеличения точности измерения времени падения шарика.

19.Исключение систематических погрешностей

Рассмотрим способы устранения систематических погрешностей.

Устранение источников погрешностей до начала измерения. Этот способ следует считать наиболее рациональным, так как он освобождает от необходимости устранять погрешности в процессе измерения или вычислять результат с учетом поправок. Так, для устранения температурной погрешности необходимо обеспечить требуемую температуру окружающей среды с допускаемыми колебаниями. Колебание температуры в заданных пределах может быть обеспечено на уровне цеха (термоконстантные цеха), лаборатории, средств измерений в целом или их отдельных частей. При измерении с помощью электронных измерительных устройств их рекомендуется прогревать.

Для устранения влияния на точность измерений внешних магнитных и электрических полей используются различные экраны.

Влияние вредных вибраций на точность измерений может быть устранено за счет использования различного рода амортизаторов.

Влияние влажности и давления на точность измерений может быть исключено, если для измерений использовать, например, специальные камеры.

Для исключения систематических погрешностей в процессе измерения существуют различные способы и приемы без использования специальных установок.

Способ введения поправок основан на знании систематической погрешности и закономерности ее изменения. В этом случае в результат измерения, содержащий систематические погрешности, вносят поправки, равные этим погрешностям, но с обратным знаком.

Так, к линейным шкалам универсального микроскопа прилагается аттестат, в котором указаны значения и знак поправки для каждого деления шкалы. Однако необходимо отметить, что как сами источники, так и условия возникновения систематических погрешностей в той или иной мере изменяются. Поэтому постоянство значений всякой систематической погрешности при повторных измерениях будет соблюдаться в определенных пределах, за которыми будут иметь место отклонения, носящие случайный характер. Если, например, систематическую погрешность исключить введением поправки, то случайные отклонения значений погрешности от значений поправки останутся не исключенными.

Способ замещения заключается в том, что измеряемый объект заменяют известной мерой, находящейся при этом в тех же условиях, в каких находился он сам. Например, на чашку весов, предназначенную для взвешивания массы, устанавливают полный комплект гирь и уравновешивают весы произвольным грузом. Затем на чашку с гирями помешают взвешиваемую массу и снимают часть гирь для восстановления равновесия. Суммарное значение массы снятых гирь соответствует значению взвешиваемой массы (способ Д.И. Менделеева). Такой способ не только устраняет погрешность, но и сохраняет чувствительность при взвешивании различных масс.

Способ замещения используется при измерении электрических параметров - сопротивления, емкости, индуктивности. Объект измерения ставят в ту или иную измерительную цепь. Уравновешивают цепь (мост). Не изменяя схемы, заменяют измеряемый объект, включая в цепь меру переменного значения. Снова уравновешивают цепь. Определяют значение измеряемой величины.

Способ компенсации погрешности по знаку заключается в том, что измерение производят дважды так, чтобы неизвестная по размеру погрешность входила в результаты с противоположными знаками. Например, с целью исключения погрешности измерения угла конуса на инструментальном микроскопе, связанную со смешения оси центров, в которых устанавливается конус, производят измерение угла сначала по одной образующей (совмещая горизонтальную линию штриховой измерительной головки с образующей конуса), а затем с другой стороны. Пусть а{ и а, - результаты двух измерений; Д - систематическая погрешность (смешение оси центров), значение которой неизвестно; аа - значение угла конуса, свободное от данной погрешности. Тогда, например, а{ = ^+Д,аа,= аа - А.

Способ противопоставления имеет большое сходство со способом компенсации по знаку. Он заключается в том, что измерения проводят два раза, причем так, чтобы причина, вызывающая погрешность, при первом измерении оказывала противоположное действие на результат второго. Например, при взвешивании на равноплечих весах для исключения погрешности от остаточной неравноплечести при первом взвешивании массу х помешают на одну чашку весов, уравновешивают гирями с обшей массой тл, помешенную на другую чашку. Тогда х =^-тх, где - действительное отношение плеч.

Затем взвешиваемую массу перемешают на ту чашку, где находились гири, а гири - на ту, где находилась масса. Так как отношение плеч і- не точно равно единице, равновесие достигается при использовании гирь обшей массой ,

Разделив первое равенство на второе, получим

если тл и пи отличаются друг от друга незначительно,

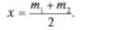
Способ применяется в тех случаях, когда сравнивается измеряемая величина с мерой примерно равного значения.