ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. 1.Движение тела массой 1 кг задано уравнением s = 6t3 + 3t + 2

1.Движение тела массой 1 кг задано уравнением s = 6t³ + 3t + 2. Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды.

Решение. Мгновенную скорость находим как производную от пути по времени: , . Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени: , . Сила, действующая на тело, определяется по второму закону Ньютона: , где , согласно условию задачи, ускорение в конце второй секунды. Тогда 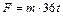, Н.

Ответ: , , Н.

2. Стержень длиной 1 м движется мимо наблюдателя со скоростью на 20% меньше скорости света. Какой покажется наблюдателю его длина?

Решение. Зависимость длины тела от скорости в релятивистской механике выражается формулой: , где l₀ – длина покоящегося стержня; 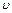– скорость его движения; с – скорость света в вакууме. Подставляя в формулу для l₀ числовые значения, имеем: l = 0,6 м.

Ответ: l = 0,6 м.

3. Две частицы движутся навстречу друг другу со скоростями: 1) 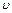= 0,5с и u = 0,75с; 2) = с и u = 0,75с. Найти их относительную скорость в первом и втором случаях.

Решение. Согласно теореме о сложении скоростей тел, движущихся навстречу друг другу, в теории относительности: , где 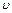, u – скорости соответственно первого и второго тел; – их относительная скорость; с – скорость света в вакууме. Для первого и второго случаев находим:

Это подтверждает, что, во-первых, ни в какой инерциальной системе отсчета скорость процесса не может превзойти скорость света, и, во-вторых, скорость распространения света в вакууме абсолютна.

Ответ: = 0,91с; = с.

4. На двух шнурах одинаковой длины, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол a=60°, и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию, израсходованную на деформацию шаров при ударе.

Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью u. Закон сохранения количества движения при этом ударе имеет вид:

. (1)

Здесь и – скорости шаров до удара. Скорость большого шара до удара равна нулю ( = 0). Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на угол 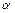ему сообщается потенциальная энергия, которая затем переходит в кинетическую: . Следовательно: . Из геометрических построений следует: , поэтому:

. (2)

Из уравнений (1) и (2) находим скорость шаров после удара:

. (3)

Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную:

, (4)

где h – высота поднятия шаров после столкновения. Из формулы (4) находим ,или с учетом (3) и подставив числовые данные получим h = 0,044 м. При неупругом ударе шаров часть энергии расходуется на их деформацию. Энергия деформации определяется разностью кинетических энергий до и после удара:

. Используя уравнения (2) и (3), получаем: , Дж.

Ответ: h = 0,044 м, DE_Д = 1,3 Дж.

5.Молот массой 70 кг падает с высоты 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием 1330 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на деформацию изделия. Систему молот–изделие–наковальня считать замкнутой.

Решение. По условию задачи, система молот–изделие–наковальня считается замкнутой, а удар неупругий. На основании закона сохранения энергии можно считать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии системы до и после удара. Считаем, что во время удара изменяется только кинетическая энергия тел, т. е. незначительным перемещением тел по вертикали во время удара пренебрегаем. Тогда для энергии деформации изделия имеем:

, (1)

где 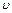– скорость молота в конце падения с высоты h; – общая скорость всех тел системы после неупругого удара. Скорость молота в конце падения с высоты h определяется без учета сопротивления воздуха и трения по формуле:

. (2)

Общую скорость всех тел системы после неупругого удара найдем, применив закон сохранения количества движения: . Для рассматриваемой системы закон сохранения количества движения имеет вид , откуда:

. (3)

Подставив в формулу (1) выражения (2) и (3), получим: , Дж.

Ответ: Дж.

6. Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением s = 2t²+4t+1. Определить работу силы за 10 сек от начала ее действия и зависимость кинетической энергии от времени.

Решение. Работа, совершаемая силой, выражается через криволинейный интеграл:

. (1)

Сила, действующая на тело, из II закона Ньютона равна: или (мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной от пути по времени). В соответствии с этим находим:

, (2), , (3)

. (4)

Из выражения (2) определим ds:

(5)

Подставив (4) и (5) в уравнение (1), получим: По этой формуле определим работу, совершаемую силой за 10 сек от начала ее действия: 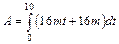, А = 960 Дж. Кинетическая энергия определяется по формуле:

. (6)

Подставляя (2) в (6), имеем: .

Ответ: А = 960 Дж, Т = m(8t²+16t+8).

7. Протон движется со скоростью 0,7с (с – скорость света). Найти количество движения и кинетическую энергию протона.

Решение. Количество движения протона определяется по формуле:

. (1)

Так как скорость протона сравнима со скоростью света, то необходимо учесть зависимость массы от скорости, воспользовавшись релятивистским выражением для массы:

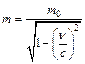, (2)

где m – масса движущегося протона; m₀ =1,67×10^{-27 кг – масса покоя протона;} v – скорость движения протона; c = 3×10⁸ м/с – скорость света в вакууме; v/c = b – скорость протона, выраженная в долях скорости света. Подставляя уравнение (2) в (1) получаем: , кг×м/с. В релятивистской механике кинетическая энергия частицы определяется как разность между полной энергией Е и энергией покоя Е₀ этой частицы:

. (3)

Ответ: p = 4,91×10^{-19 кг}×м/с, Т = 0,6×10^-10 Дж.

8. Тонкий стержень вращается с угловой скоростью 10 с^-1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. В процессе вращения в той же плоскости стержень перемещается так, что ось вращения проходит через его конец. Найти угловую скорость после перемещения.

Решение. Используем закон сохранения момента импульса: , где J_i, – момент инерции стержня относительно оси вращения. Для изолированной системы тел векторная сумма моментов импульса остается постоянной. В данной задаче вследствие того, что распределение массы стержня относительно оси вращения изменяется, момент инерции стержня также изменится. В соответствии с законом сохранения момента импульса запишем:

. (1)

Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен:

. (2)

По теореме Штейнера: где J – момент инерции тела относительно произвольной оси вращения; J₀ – момент инерции относительно параллельной оси, проходящей через центр масс; d – расстояние от центра масс до выбранной оси вращения. Найдем момент инерции относительно оси, проходящей через его конец и перпендикулярной стержню:

. (3)

Подставляя, формулы (2) и (3) в (1), имеем: , откуда .

Ответ: w₂ = 2,5 c^-1.

9. Маховик массой 4 кг вращается с частотой 720 мин^-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения:

, (1)

где J – момент инерции маховика относительно оси, проходящей через центр масс; – изменение угловой скорости за промежуток времени . По условию, , где 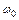– начальная угловая скорость, так как конечная угловая скорость = 0. Выразим начальную угловую скорость через частоту вращения маховика; тогда и Момент инерции маховика , где m – масса маховика; R – его радиус. Формула (1) принимает вид: откуда М = -1,61 Н×м. Знак «-» говорит о том, что момент томозящий.

Угол поворота (т. е. угловой путь ) за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения:

, (2)

где – угловое ускорение. По условию, , , . Тогда выражение (2) можно записать так: . Так как j = 2pN, w₀ = 2pn, то число полных оборотов маховика: .

Ответ: М = 1,61 Н×м, N = 180.

10. В сосуде объемом 2 м³ находится смесь 4 кг гелия и 2 кг водорода при температуре 27 °С. Определить давление и молярную массу смеси газов.

Решение. Воспользуемся уравнением Клайперона-Менделеева, применив его к гелию и водороду:

, (1)

, (2)

где P₁ – парциальное давление гелия; m₁ – масса гелия; – его молярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль×К) – молярная газовая постоянная; P₂ - парциальное давление водорода; m₂ – масса водорода; – его молярная масса. Под парциальным давлением P₁ и P₂ понимается то давление, которое производил бы газ, если бы он находился в сосуде один. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:

. (3)

Из уравнения (1) и (2) выразим P₁ и P₂ и подставим в уравнение (3). Имеем:

. (4)

Молярную массу смеси газов найдем по формуле: , где v₁ и v₂ – число молей гелия и водорода соответственно. Число молей газов определим по формулам: и . Тогда: . Подставляя числовые значения получаем: P = 2493 КПа и 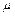= 3×10^-3 кг/моль.

Ответ: P = 2493 КПа, 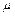=3×10^-3 кг/моль.

11. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 2 кг водорода при температуре 400 К?

Решение. Считаем водород идеальным газом. Молекула водорода двухатомная, связь между атомами считаем жесткой. Тогда число степеней свободы молекулы водорода равно 5, три из которых поступательные и две вращательные. В среднем на одну степень свободы приходится энергия , где k – постоянная Больцмана; Т – термодинамическая температура. Для одной молекулы: и . Число молекул, содержащихся в массе газа: . Тогда средняя кинетическая энергия поступательного движения молекул двух килограмм водорода: . Средняя кинетическая энергия вращательного движения этих же молекул: . Подставляя числовые значения имеем: =4986 КДж и =2324 КДж.

Ответ: =4986 КДж, =2324 КДж.

12. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27 ⁰С и давлении 100 кПа.

Решение. Средняя длина свободного пробега молекул кислорода вычисляется по формуле: , где d – эффективный диаметр молекулы кислорода; n – число молекул в единице объема, которое можно определить из уравнения: , где k – постоянная Больцмана. Таким образом, имеем: . Число соударений Z, происходящих между всеми молекулами за 1 с, равно: , где N – число молекул кислорода в сосуде объемом 2×10^{-3 м3}; <Z> – среднее число соударений одной молекулы за 1 с. Число молекул в сосуде: . Среднее число соударений молекулы за 1 с равно: , где <V> – средняя арифметическая скорость молекулы. Тогда выражение для Z перепишется как: . Подставляя числовые значения, получим: Z = 9×10²⁸ с^-1, = 3,56×10⁸ м.

Ответ: Z = 9×10²⁸ с^-1, = 3,56×10⁸ м.

13. Определить коэффициенты диффузии и внутреннего трения азота, находящегося при температуре Т = 300 К и давлении 10⁵ Па.

Решение. Коэффициент диффузии определяется по формуле: , где <V> – средняя арифметическая скорость молекул, – средняя длина свободного пробега молекул. Для нахождения воспользуемся формулой из решения примера 12: 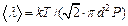. Выражение для коэффициента диффузии примет вид: . Коэффициент внутреннего трения: , где r – плотность газа при температуре 300 К и давлении 10⁵ Па. Для нахождения r воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота: при нормальных условиях Т₀=273 К, P=1,01×10⁵ Па и в условиях задачи: и . Учитывая, что и , имеем: . Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии: . Подставляя числовые значения, получим: D = 4,7×10⁵ м²/с и h = 5,23×10^-5 кг/(м×с).

Ответ: D = 4,7×10⁵ м²/с и h = 5,23×10^-5 кг/(м×с).

14. Кислород массой 160 г нагревают при постоянном давлении от 320 до 340 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа.

Решение. Количество теплоты, необходимое для нагревания газа при постоянном давлении: . Здесь с_р и С_р – удельная и молярная теплоемкости газа при постоянном давлении; m =32×10^-3 кг/моль – молярная масса кислорода. Для всех двухатомных газов: , Дж/(моль×К). Изменение внутренней энергии газа находим по формуле: , где С_V – молярная теплоемкость газа при постоянном объеме. Для всех двухатомных газов: С_V = = 5/2×R; С_V = 20,8 Дж/(моль×К). 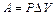Работа расширения газа при изобарном процессе: , где – изменение объема газа, которое можно найти из уравнения Клайперона–Менделеева. При изобарном процессе: и . Почленным вычитанием выражений находим: , следовательно: . Подставляя числовые значения, получаем: Дж, Дж, Дж.

Ответ: Дж, Дж, Дж.

15. Объем аргона, находящегося при давлении 80 кПа, увеличился от 1 до 2 л. На сколько изменится внутренняя энергия газа, если расширение производилось: а) изобарно; б) адиабатно.

Решение. Применим первый закон термодинамики. Согласно этому закону, количество теплоты Q, переданное системе, расходуется на увеличение внутренней энергии и на внешнюю механическую работу А: . Величину системы можно определить, зная массу газа, удельную теплоемкость при постоянном объеме с_V и изменение температуры : . Однако удобнее изменение внутренней энергии определять через молярную теплоемкость С_V, которая может быть выражена через число степеней свободы: . Подставляя величину С_V получаем: . Изменение внутренней энергии зависит от характера процесса, при котором идет расширение газа. При изобарном расширении газа, согласно первому закону термодинамики, часть количества теплоты идет на изменение внутренней энергии . Найти для аргона по полученной формуле нельзя, так как масса газа и температура в условии задачи не даны. Поэтому необходимо провести преобразование этой формулы. Запишем уравнение Клайперона-Менделеева для начального и конечного состояний газа: и , или . Тогда: . Это уравнение является расчетным для определения при изобарном расширении. При адиабатном расширении газа теплообмена с внешней средой не происходит, поэтому Q = 0. Первое начало термодинамики запишется в виде: . Это соотношение устанавливает, что работа расширения газа может быть произведена только за счет уменьшения внутренней энергии газа (знак минус перед ): . Формула работы для адиабатного процесса имеет вид: , где g – показатель адиабаты, равный: . Для аргона – одноатомного газа (i= 3) – имеем g =1,67. Находим изменение внутренней энергии при адиабатном процессе для аргона: . Для определения работы расширения аргона формулу для следует преобразовать, учитывая параметры, данные в условии задачи. Применив уравнение Клайперона-Менделеева для данного случая , получим выражение для подсчета изменения внутренней энергии: . Подставляя числовые значения, имеем: а) при изобарном расширении Дж; б) при адиабатном расширении Дж.

Ответ: а) =121 Дж; б) = -44,6 Дж.

16. Температура нагревателя тепловой машины 500 К. Температура холодильника 400 К. Определить к.п.д. тепловой машины, работающей по циклу Карно, и полную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты.

Решение. Коэффициент полезного действия машины определяется по формуле: или . Из этих выражений находим: . Произведем вычисления: A = 335 Дж. Эта работа совершается за 1 с, следовательно, полная мощность машины равна 335 Вт.

Ответ: = 0,2, N =335 Вт.

17. Горячая вода некоторой массы отдает теплоту холодной воде такой же массы и температуры их становятся одинаковыми. Показать, что энтропия при этом увеличивается.

Решение. Пусть температура горячей воды Т₁, холодной Т₂, а температура смеси . Определим температуру смеси, исходя из уравнения теплового баланса: или , откуда: . Изменение энтропии, происходящее при охлаждении горячей воды: . Изменение энтропии, происходящее при нагревании холодной воды: . Изменение энтропии системы равно: или ; так как и 4T₁T₂>0, то .