Постановка и экономико-математическая модель транспортной задачи

Транспортная задача относится к классу задач линейного программирования. Транспортная задача решает проблему нахождения оптимального (минимального) по стоимости плана распределения и перемещения ресурсов от производителей к потребителям. Проблема оптимизации стоимости перевозок актуальна и на сегодняшний день, так как позволяет фирмам и предприятиям существенно сократить расходы на транспорт. Правильная организация перевозок позволяет устранить встречные и дублирующие перевозки, сократить количество дальних перевозок. При решении транспортной задачи необходимо:

· Обеспечить всех потребителей ресурсами.

· Распределить все произведенные ресурсы.

· Переместить ресурсы от производителей к потребителям с наименьшими затратами.

Имеется m пунктов производства А1…Аm однородного продукта и n пунктов потребления B1…Bn этого продукта. Для каждого пункта производства Ai задан объем производства ai, для каждого Bj – bj. Из каждого пункта производства в каждый пункт потребления возможна транспортировка.

Транспортные издержки перевозки из Ai в Bj = Cij. Требуется составить такой план перевозки, что:

1) – Транспортные издержки минимальны

2) – Все запросы удовлетворены.

3) – Из каждого пункта производства вывезен весь продукт.

Пусть Xij – количество продукта, перевезенного из Ai в Bj. Тогда:

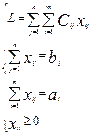Транспортная задача имеет допустимое решение тогда и только тогда, когда 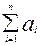= 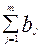(условие баланса) , когда оно выполняется, задача называется замкнутой, иначе – открытой.

Возможны два варианта открытых задач:

1) - 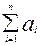< 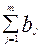, объем производства меньше объема потребления. Добавляем фиктивный пункт производства 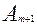, 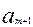= 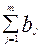- 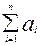стоимость перевозок из 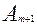равна штрафу за недопоставку продукции. В постановке задачи m меняем на m+1.

2) - 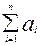> 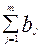, аналогично, добавляем пункт потребления.

Замечание: таким образом открытая ТЗ всегда может быть сведена к закрытой. При этом фиктивные перевозки определяют либо объем перепроизводства для ai или объем недопоставок для bj.