
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод потенциалов в решении ТЗ линейного программирования.
Будем рассматривать невырожденную замкнутую ТЗ. Метод потенциалов (МП) является модификацией симплекс-метода. Для пунктов производства и потребления вводятся потенциалы в виде целых чисел:
 , где
, где  - числа, которые могут быть как положительными, так и отрицательными.
- числа, которые могут быть как положительными, так и отрицательными.
 =
=  - псевдостоимость.
- псевдостоимость.
Потенциалы выбираются таким образом, чтобы псевдостоимость была  £
£ 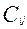 .
.
Теорема 1: Для заданных потенциалов  и
и  суммарная псевдостоимость
суммарная псевдостоимость 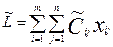 сохраняет значение для любого допустимого плана
сохраняет значение для любого допустимого плана  .
.
Теорема 2: Если для всех базисных клеток плана  можно подобрать такое значение
можно подобрать такое значение  , что :
, что :
(*)  =
=  =
= 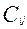 , а для всех свободных клеток:
, а для всех свободных клеток:
 =
=  £
£ 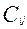 , то данный план
, то данный план  является оптимальным.
является оптимальным.
Формальное описание метода потенциалов.
1) Методом северо-западного угла или методом минимального элемента строится начальный опорный план
2) Для полученного опорного плана определяются потенциалы, исходя из условия  =
= 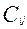 для
для  >0 так как в опорном плане таких клеток (m+n-1), то мы получим систему из (m+n-1) уравнений с (m+n) неизвестными, поэтому чаще всего берут a1=0 и производят вычисление потенциалов
>0 так как в опорном плане таких клеток (m+n-1), то мы получим систему из (m+n-1) уравнений с (m+n) неизвестными, поэтому чаще всего берут a1=0 и производят вычисление потенциалов
3) Для всех свободных клеток подсчитывают  =
=  . Если
. Если  £
£ 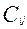 , то полученный план оптимален.
, то полученный план оптимален.
4) Иначе Выбирается свободная клетка, где  >
> 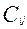 явл. max(
явл. max(  -
- 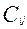 ), начиная с этой точки строим цикл перерасчета, тоесть замкнутую ломаную линию проходящую через некоторые базовее клетки и возвращающуюся в эту-же свободную, причем в базисной клетке ломаная сворачивает на 90 (прямоугольник). Для любой свободной клетки существует единственный такой цикл.
), начиная с этой точки строим цикл перерасчета, тоесть замкнутую ломаную линию проходящую через некоторые базовее клетки и возвращающуюся в эту-же свободную, причем в базисной клетке ломаная сворачивает на 90 (прямоугольник). Для любой свободной клетки существует единственный такой цикл.
5) Клетки, стоящие в цикле на нечетных местах начиная от свободной назовем отрицательными и пометим (-), на четных – положительными (+). Перевозки, соответствующие (-) будем уменьшать, а (+) соответственно увеличивать. В каждом столбце и строке число клеток (+) равно числу (-), поэтому суммы строк и столбцов не изменятся.
Для того, чтобы план оставался допустимым, необходимо, чтобы одна из базисных переменных стала свободной, Q=min(Xst), где Xst – отрицательные клетки цикла.
Далее делаем перерасчет:
Все (+) клетки цикла Xml=Xml+Q;
Все (-) клетки цикла Xst=Xst-Q;
Все оставшиеся клетки, не присутствовавшие в цикле на углах переносятся с прежними значениями.
Замечание: Каждая итерация метода потенциалов приводит к уменьшению целевой функции
Lold-Lnew = Q(  -
- 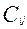 ).
).
Дата добавления: 2015-01-19; просмотров: 270; Мы поможем в написании вашей работы!; Нарушение авторских прав |