Статическая детерминированная модель без дефицита.

Простейшие модели управления запасами характеризуются постоянным во времени спросом, мгновенным пополнением склада и отсутствием дефицита.

Предположение о том, что дефицит не допускается, означает полное удовлетворение спроса на запасаемый продукт, т.е. совпадение функций и .

Пусть

- общее потребление запасаемого продукта за рассматриваемый интервал времени - .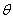

Предполагается, что расходование запаса происходит непрерывно с постоянной интенсивностью, т.е. , а пополнение запаса происходит партиями одинакового объема, т.е. функция не является непрерывной.

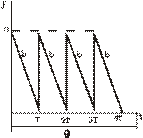
Графически уровень запаса в зависимости от времени представлен на рис.

На временном интервале уровень запаса уменьшается по прямой 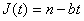от значения n до нуля. Так как дефицит не допускается, то в момент Т уровень запаса мгновенно пополняется до прежнего значения n за счет поступления партии заказа. И так процесс изменения повторяется на каждом временном интервале продолжительностью Т.

(3) (4)

Задача управления запасами состоит в определении такого объема партии , при котором суммарные затраты на создание и хранение запаса были бы минимальными.

Обозначим:

С - суммарные затраты

С₁ - затраты на создание запаса

С₂ - затраты на хранение запаса

c₁-затраты на доставку одной партии продукта, не зависящие от объема партии

с₂ - затраты на хранение одной единицы продукта в единицу времени

Функция суммарных затрат: (5)

В точке минимума функции C(n) ее производная

, (6)

откуда формула наиболее экономичного объема партии, называемая формулой Уилсона:

(7) или (8)

Время расхода оптимальной партии:

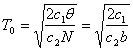(9) или ₍10)

В действительности пополнение запаса не может произойти мгновенно в момент размещения заказа, как предполагалось ранее. Для большинства реальных ситуаций существует положительный срок выполнения заказа – время доставки заказа, [ед.t], от момента его размещения до реальной поставки. размер запаса на складе, при котором надо подавать заказ на доставку очередной партии, [ед.тов.] обозначается как – точка заказа.

(11)

Пример 2Неоновые лампы в университетском городке заменяются с интенсивностью 100 штук в день. Подразделение материального обеспечения городка заказывает эти лампы с определенной периодичностью. Стоимость размещения заказа на покупку ламп составляет 100 долл. Стоимость хранения лампы на складе оценивается в 0,02 долл. в день. Срок выполнения заказа от момента его размещения до реальной поставки равен 8 дней. Требуется определить оптимальную стратегию заказа неоновых ламп.

На основании приведенных данных имеем следующее. b=100 штук/ день, с1=100$, c2=0,02$ в день, =12 дней. Следовательно ламп. Время расхода оптимальной партии: дней, ламп.