Уравнение первого закона термодинамики для потока газа

Аналитическое выражение первого закона термодинамики (2.14) было записано для процессов, в которых не происходит перемещение газа в пространстве. В случае, если газ наряду с расширением или сжатием еще и перемещается в пространстве, то необходимо учитывать изменение его внешней кинетической энергии. В этом случае уравнение первого закона термодинамики для потока газа принимает вид

(2.28)

где w - скорость потока; dw²/2 - изменение кинетической энергии газового потока.

В интегральной форме . (2.29)

Если газу, при его движении, не сообщается тепло (dq=0), то уравнение (2.28) принимает вид

(2.30)

В интегральной форме

. (2.31)

Из уравнений (2.30) и (2.31) следует, что при движении газа через канал без теплообмена с внешней средой приращение кинетической энергии происходит за счет уменьшения его энтальпии.

Представим схему прямого цикла. Пусть имеется тело А с температурой Т₁ (горячий источник теплоты) и тело В с температурой Т₂ (холодный источник теплоты), (рис. 3.2). Следовательно, Т₁ > Т₂.

Имеется также рабочее тело, которое может совершать процессы расширения и сжатия. Рабочее тело получает q₁ тепла и за счет этого расширяется по линии 1а2. В ходе сжатия по линии 2в1 рабочее тело отдает холодному источнику q₂ тепла. Т.к. рабочее тело в конечном итоге возвращается в исходное положение 1, то изменение внутренней энергии за цикл будет равно нулю, т.е.

Du_ц = 0.

Тогда, согласно первому закону термодинамики:

q₁ - q₂ = l_ц, (3.2)

где l_ц - полезная работа за цикл.

Степень совершенства прямого цикла оценивается термическим к.п.д. цикла h_t :

. (3.3)

Термическим к.п.д. цикла называют отношение тепла, перешедшего в полезную работу, ко всему теплу, затраченному на совершение цикла. Термический к.п.д. измеряют в процентах или долях единицы.

Представим схему обратного цикла. Пусть имеется тело А с температурой Т₁ (горячий источник) и тело В с температурой Т₂ (холодный источник)
(рис. 3.3). Имеется рабочее тело. Причем Т₁ > Т₂. Для осуществления процесса расширения 1а2 от холодного источника подводится к рабочему телу q₂ тепла. В процессе сжатия 2в1 от рабочего тела отводится к горячему источнику q₁
тепла. Причем q₁ > q₂. Для того чтобы такой цикл был возможен, необходимо затратить работу l_ц = l_сж - l_расш. При этом отведенное от рабочего тела тепло q₁ будет больше подведенного к нему тепла на величину затраченной работы:

q₁ = q₂ + l_ц.

Степень совершенства такого цикла оценивается холодильным коэффициентом e_t, представляющим отношение количества тепла взятого у холодного источника q₂, к затраченной работе l_ц .

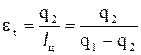. (3.4)

Прямой цикл Карно. Наивыгоднейший теоретический цикл теплового двигателя, преобразующий между заданными температурами рабочего тела максимальное количество теплоты в работу, был предложен в 1824 году французским ученым Сади Карно.

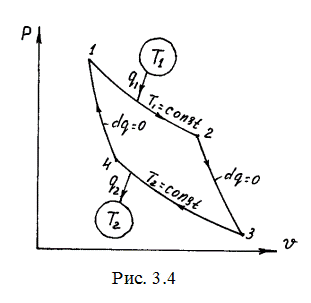
Цикл Карно может быть представлен следующим образом (рис. 3.4). Имеются два источника тепла: высший с температурой Т₁ и низший с температурой Т₂. Источники тепла предполагаются бесконечно большими, так что отвод тепла от высшего и сообщение тепла низшему источнику не изменяют их температур. Пусть в цилиндре под поршнем, движущимся без трения, находится в равновесии 1 кг рабочего тела. Это состояние изобразится в p, u - координатах точкой 1. Рабочее тело приводится во взаимодействие с высшим источником и расширяется при
Т₁ = const, получая от источника q₁ тепла. В точке 2 рабочее тело разобщается с источником тепла и дальнейшее расширение происходит без теплообмена с окружающей средой, т.е. адиабатно. В точке 3 процесс расширения заканчивается и начинается процесс сжатия. Рабочее тело сообщается с низшим источником тепла и от точки 3 до точки 4 происходит изотермическое сжатие при Т₂ = const. При этом рабочее тело отдает низшему источнику q₂ тепла. В точке 4 рабочее тело разобщается с низшим источником и дальнейшее сжатие от точки 4 до точки 1 происходит адиабатно. Таким образом, прямой цикл Карно состоит из следующих процессов: 1-2 - изотермическое расширение; 2-3 - адиабатное расширение; 3-4 - изотермическое сжатие; 4-1 - адиабатное сжатие.

Можно доказать (доказательство приведено в п.3.2 этой главы), что термический к.п.д. цикла Карно

. (3.5)

Выражение (3.5) позволяет сделать следующие выводы.

1. Термический к.п.д. цикла Карно не зависит от природы рабочего тела, т.к. отсутствуют специальные характеристики, присущие отдельным рабочим телам. Это положение известно как теорема Карно.

2. Термический к.п.д. обратимого цикла Карно полностью определяется значениями абсолютных температур горячего и холодного источников. Повышение к.п.д. возможно путем увеличения разности (перепада) температур Т₁ и Т₂.

3. Термический к.п.д. цикла Карно и, следовательно, любого другого цикла всегда меньше единицы, т.к. Т₁ ¹ ¥ и Т₂ ¹ 0 К. Значит, все тепло, подведенное к рабочему телу, невозможно полностью превратить в полезную работу.

4. Термический к.п.д. цикла Карно равен нулю при Т₁ = Т₂, т.е. получение полезной работы возможно лишь при наличии двух источников тепла с различными температурами.