Политропный процесс. Выведем уравнение политропного процесса

Выведем уравнение политропного процесса. Для этого введем понятие о политропной теплоемкости - с. Тогда dq = cdT. С учетом этого запишем уравнения первого закона термодинамики (2.24) и (2.16)

сdТ = c_pdT -udp,

сdТ = c_udT + pdu ,

откуда . Обозначим - показатель политропы.

Тогда последнее уравнение запишется:

npdu = - udp. (а)

Разделив уравнение (а) на pu, запишем Проинтегрировав это уравнение, получим n ln u + ln p = const или ln puⁿ = const.

Откуда получим уравнение политропы

puⁿ = const. (4.28)

Политропным называется такой процесс изменения состояния рабочего тела, в котором показатель политропы n остается постоянным на протяжении всего процесса.

Формулы соотношения параметров газа в политропном процессе, которые являются следствием уравнений puⁿ = const и pu = RT, очевидно, будут иметь тот же вид, что и выведенные выше в адиабатном процессе, но только в них показатель адиабаты к нужно заменить показателем политропы n:

; и .

Изменение внутренней энергии Du и энтальпии Dh в политропном процессе, как и в любом термодинамическом процессе, найдется по уравнениям

Du = u₂ - u₁ = c_u(T₂ - T₁) и Dh = h₁ - h₂ = c_p(T₂ - T₁).

Формулы для работы изменения объема могут быть найдены по уравнению , куда подставляют р = р₁u₁ⁿ/vⁿ, где p и u - текущие значения параметров.

В результате интегрирования получим

. (4.29)

Выражение (4.29), аналогичное адиабатному процессу, можно представить как

, (4.30)

и . (4.31)

Формула для технической работы согласно уравнению (а) l¢ = nl, т.е.

. (4.32)

Теплоемкость газа в политропном процессе можно найти из равенства
n = (c - c_p)/(c - c_u). Откуда имеем nc - nc_u= c - c_p или nc - c = nc_u - кc_u отсюда
с(n-1) = c_u(n-к). Окончательно получим

. (4.33)

Теплоемкость газа в политропном процессе в зависимости от значения показателя политропы n может быть положительной, отрицательной, равной нулю или бесконечности.

Количество тепла, участвующего в процессе:

. (4.34)

Политропный процесс является обобщающим для всех ранее рассмотренных процессов. В этом нетрудно убедиться, подставляя в выражение
n = (c - c_p)/(c - c_u) значения соответствующих политропных теплоемкостей:

1) для изохорного процесса

с = с_u; . Уравнение puⁿ = const представим в виде , тогда .

Следовательно, при n = ±¥ уравнение политропы обратилось в уравнение изохоры;

2) для изобарного процесса

с = с_р; ; ;

3) для изотермического процесса

.

Следовательно, n - 1 = 0; n=1 и puⁿ = pu = const;

4) для адиабатного процесса

с=0; ; puⁿ = pu^к = const.

Если в координатах p, u выбрать произвольную точку А (рис. 4.9) и провести из т.А все рассмотренные выше процессы, а также сколько угодно других процессов, в которых показатель политропы меняется от +¥ до - ¥, то можно по графику процесса сказать о знаках работы, теплоты и изменения внутренней энергии, а также о знаке показателя n (как это показано на
рис. 4.9). Так, например, во всех процессах, исходящих из точки А и идущих правее адиабаты теплота, будет подводиться к рабочему телу q>0, а в противоположной области отводиться q<0 и т.д.

Изменение энтропии в политропном процессе или в интегральной форме

. (4.35)

Представим основные процессы как частные случаи политропного процесса в координатах T, s (рис. 4.10). Области положительной и отрицательной работы, теплоты и изменения внутренней энергии показаны на рисунке. Показатель политропы n может быть определен, если известны параметры двух точек процесса. , отсюда 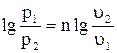. Тогда или . В литературе также приводятся чисто графические способы определения показателя политропы.