Адиабатный процесс. Процессы, протекающие без теплообмена рабочего тела с окружающей средой, называются адиабатными процессами (dq = 0 и q =0)

Процессы, протекающие без теплообмена рабочего тела с окружающей средой, называются адиабатными процессами (dq = 0 и q =0). Линия, изображающая адиабатный процесс, называется адиабатой.

Для вывода уравнения адиабатного процесса используем уравнения первого закона термодинамики (2.24) и (2.16)

c_pdT -udp = 0

c_udT + pdu= 0,

откуда 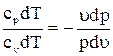или 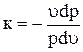, отсюда кpdu = - udp. (a)

Левую и правую часть уравнения (а) разделим на pu и запишем

. (в)

Проинтегрировав уравнение (в), получим

к lnu+ lnp = const,

или ln pu^к = const.

Если логарифм какой-то величины const, то и сама величина будет const. Отсюда получаем уравнение адиабаты

pu^к = const. (4.16)

Из аналитической геометрии известно, что уравнение (4.16) является уравнением неравнобокой гиперболы (рис. 4.7). На рисунке 1-2 - расширение, 1-3 - сжатие.

На рисунке для сравнения изображена также изотерма. Т.к. к > 1, поэтому адиабата проходит всегда круче, чем изотерма. Найдем соотношения между параметрами в адиабатном процессе:

а) p = f(u). Из уравнения адиабаты
p₁u₁^к = p₂u₂^к. Следовательно,

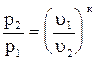или 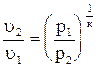; (4.17)

б) Т = f(u). Записав уравнение состояния в виде p = RT/u, подставим его в уравнение адиабаты (4.16) и получим RТu^к/u = const. Поскольку R для данного газа const, то, поделив на R последнее уравнение в его правой части, получим новую const.

Tu^к-1 = const. (4.18)

Из уравнения (4.18) получим 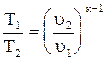; (4.19)

в) T = f(p). Записав уравнение состояния в виде u = RT/p, подставим его в уравнение адиабаты (4.16) и получим R^кT^кp/p^к = const. Поделив это уравнение на R^к, получим Т^кр^1-к = const. Извлекая корень к-й степени, получаем 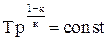. Откуда 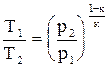или . (4.20)

Изменение внутренней энергии Du = c_u(T₂ - T₁).

Работу изменения объема найдем из уравнения первого закона термодинамики du + dl = 0, отсюда dl = - du,

или l = - (u₂ - u₁) - u₁ - u₂ = c_u(T₁ - T₂). (4.21)

То есть работа адиабатного расширения совершается в результате изменения внутренней энергии рабочего тела, которая уменьшается на величину, эквивалентную совершенной работе. При отрицательной работе (работе сжатия) внутренняя энергия возрастает на величину затраченной работы.

Подставив в уравнение (4.21) значение с_u = R/(к-1), получим

. (4.22)

Заменив в уравнении (4.22) произведения RT₁ = p₁u₁ и RT₂ = p₂u₂ по уравнению состояния, получим

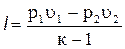. (4.23)

Уравнение (4.23) может быть представлено в следующем виде:

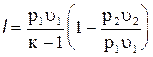, помня, что по (4.17)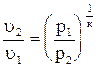 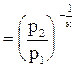, получим

. (4.24)

Так как по уравнению (а) крdu = - udp, то следовательно

кdl = dl¢ или l¢ = кl. (4.25)

Отсюда техническая работа

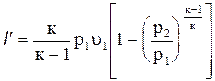. (4.26)

Если говорить о теплоемкости в адиабатном процессе, то, очевидно,
c = dq/dT =0, т.к. dq = 0.

Адиабатный процесс является изоэнтропийным процессом, т.к. для него

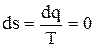и Ds = s₂ - s₁ = 0. ( 4.27)

В координатах T, s адиабата вертикальная прямая: 1-2 - расширение, 1-3 - сжатие (рис. 4.8).