
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Выявление общей тенденции в рядах динамики.
Влияния эволюционного характера –это изменения , определяющие некое общее направление развития. Такие изменения динамического ряда называют тенденцией развития или трендом. Выравнивание ряда динамики позволяет представить изменения явления как функцию времени. Наиболее распространенными методами выявления в ряду динамики являются:
1)укрупнение периодов
2)расчет скользящей средней
3)аналитическое выравнивание
Преобразуем показатели урожайности в горизонтальную таблицу.
Таблица 4 Динамика урожайности подсолнечника.
| Годы | |||||||||
| Урожайность ц/га | 15,89 | 13,96 | 15,29 | 10,53 | 13,45 | 20,76 | 17,39 | 17,2 | 22,12 |
Мы видим, что в развитии урожайности нет закономерности или общей тенденции. В целях более детального изучения динамики урожайности и выявления тенденции следует провести выравнивание рядов динамики, используя следующие статистические методы:
I. Укрупнение периодов, т.к. исходная информация приведена за 9 лет, то выравнивание следует производить по трехлетиям. Для этого: а) определим сумму урожайности по трехлетиям: 2001-2003=15,89+13,96+15,29=45,14;
2004-2006=10,53+13,45+20,76=44,74; 2007-2009=17,39+17,2+22,12=56,71.
б) определяется средняя урожайность по каждому трехлетию (средняя арифметическая простая): 2001-2003=45,14/3=15,06; 2004-2006=44,74/3=14,91; 2007-2009=56,71/3=18,9;
Полученных данных недостаточно для выявления общей тенденции, поэтому используем следующий метод выравнивания.
II. Расчет скользящей средней. Она будет образована по трехлетиям со сдвигом на 1 год вправо, т.к. ряд динамики расположен по горизонтали. При этом: а) определяем сумму урожайности по трехлетиям.
2001-2003=15,89+13,96+15,29=45,14;
2002-2004=13,96+15,29+10,53=39,78;
2003-2005=15,29+10,53+13,45=39,27;
2004-2006=10,53+13,45+20,76=44,74;
2005-2007=13,45+20,76+17,39=51,6;
2006-2008=20,76+17,39+17,2=55,35;
2007-2009=17,39+17,2+22,12=56,71;
б) определяется средняя скользящая урожайность по каждому трехлетию (сред. арифметическая простая)
2001-2003=45,14/3=15,06;
2002-2004=39,78/3=13,26;
2003-2005=39,27/3=13,09;
2004-2006=44,74/3=14,91;
2005-2007=51,6/3=17,2;
2006-2008=55,35/3=18,45;
2007-2009=56,71/3=18,9;
Выполненные расчеты представим в виде таблицы.
Таблица 5 Выявление тенденции в изменении урожайности подсолнечника.
| Годы | Укрупненные периоды | Скользящая средняя | ||
| Сумма за трехлетие | Средняя урожайность за трехлетие ц/га | Сумма за трехлетие | Скользящая средняя урожайность за трехлетие, ц/га | |
| 45,14 | 15,06 | 45,14 | 15,06 | |
| 39,78 | 13,26 | |||
| 39,27 | 13,09 | |||
| 44,74 | 14,91 | 44,74 | 14,91 | |
| 51,6 | 17,2 | |||
| 55,35 | 18,45 | |||
| 56,71 | 18,9 | 56,71 | 18,9 | |
| - | - |
Анализируя полученные данные можно говорить о приблизительной нарастающей тенденции. Однако данных исследований недостаточно для утверждения повышения урожайности, так в полученных данных имеются скачки показателей. В связи с этим воспользуемся следующим способом выравнивания.
III. Аналитическое выравнивание. Изобразим динамику изучаемого явления графически (приложение 2)
Для аналитического выравнивания первоначально берется уравнение прямой  , где у(t)- теоретическое значение урожайности за каждый год,t-условное обозначение периода времени,
, где у(t)- теоретическое значение урожайности за каждый год,t-условное обозначение периода времени, 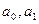 -неизвестные параметры.
-неизвестные параметры.
С целью нахождения коэффициентов регрессии решается система нормальных уравнений:
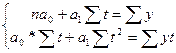
Исходные и расчетные данные для решения системы уравнений представлены в следующей таблице.
Таблица 6. Аналитическое выравнивание урожайности подсолнечника в СХА «им. Дзержинского» Павловского района
| Годы | Урожайность,ц/га (у) | Условное обозначение периода времени (t) | t2 | y*t | y(t)=16,176+0,768*t |
| 15,89 | -4 | -63,56 | 13,136 | ||
| 13,96 | -3 | -41,88 | 13,896 | ||
| 15,29 | -2 | -30,58 | 14,656 | ||
| 10,53 | -1 | -10,53 | 15,416 | ||
| 13,45 | 16,176 | ||||
| 20,76 | 20,76 | 16,936 | |||
| 17,39 | 34,78 | 17,696 | |||
| 16,2 | 48,6 | 18,456 | |||
| 22,12 | 88,48 | 19,216 | |||
| Итого | 145,59 | 46,07 | 145,584 |
Подставим итоговые строки в систему уравнений.

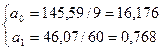
Подставим найденные значения параметров в уравнение прямой и найдем его конкретное выражение: y(t)=16,176+0,768*t
Параметр  говорит о том, что ежегодно в течении изучаемого периода урожайность подсолнечника увеличивалась на 0, 768 ц/га. Подставив значение t в уравнение прямой, найдем теоретические значения урожайности подсолнечника за каждый год.
говорит о том, что ежегодно в течении изучаемого периода урожайность подсолнечника увеличивалась на 0, 768 ц/га. Подставив значение t в уравнение прямой, найдем теоретические значения урожайности подсолнечника за каждый год.
Таким образом, мы получили выровненный ряд урожайности подсолнечника, который говорит о ее системном увеличении на 0,768 ц/га. Полученные теоретические значения отобразим на графике.
Для дальнейших исследований рассмотрим выровненные значения урожайности, а также прогнозной урожайности на 3 года по 4м видам уравнений: прямая, парабола, экспонента и S-кривая. Исходная информация представлена в приложении 3.
Расчеты оформим в виде таблиц.
Таблица 7.Выровненные значения урожайности.
| Годы | Фактическая урожайность подсолнечника,ц/га | Выровненные значения урожайности подсолнечника,ц/га | |||
| По уравнению прямой | По уравнению параболы | По уравнению экспоненты | По уравнению S-кривой | ||
| 15,89 | 13,1053 | 15,2571 | 13,2106 | 14,1634 | |
| 13,96 | 13,8731 | 14,4111 | 13,8200 | 15,3547 | |
| 15,29 | 14,6410 | 14,0261 | 14,4575 | 15,7736 | |
| 10,53 | 15,4088 | 14,1023 | 15,1244 | 15,9874 | |
| 13,45 | 16,1766 | 14,6396 | 15,8221 | 16,1170 | |
| 20,76 | 16,9445 | 15,6380 | 16,5520 | 16,2040 | |
| 17,39 | 17,7123 | 17,0975 | 17,3155 | 16,2664 | |
| 16,2 | 18,4801 | 19,0181 | 18,1143 | 16,3134 | |
| 22,12 | 19,2480 | 21,3998 | 18,9499 | 16,3501 |
Определим средние значения ряда динамики по каждому уравнению.

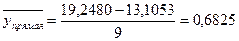
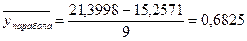
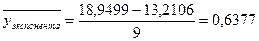

Анализируя полученные данные можно сделать вывод о том, что наиболее точно выявляют тенденцию уравнения прямой и параболы. Для наиболее точного выявления определим по показателям вариации, какое уравнение наиболее точно описывает сложившуюся тенденцию развития урожайности.
Таблица 8 Отклонение в уравнениях для выравнивания значений урожайности подсолнечника.
| Функция | Линейное отклонение | Дисперсия, ц/га | СКО, ц/га | Коэффициент вариации, % |
| 12,3375+0,767833*T | 0,00000 | 7,50337 | 2,26844 | 15,1431 |
| 16,5643-1.53769*T+0,230552*T^2 | 0,00000 | 5,68431 | 1,78473 | 11,6951 |
| Exp(2,53593+0,0450968*T) | 0,24702 | 7,33938 | 2,22057 | 14,6026 |
| Exp(2,81218-0,161513/T) | 0,33994 | 10,8200 | 2,58802 | 16,7631 |
Наиболее точно, согласно таблицы 8(приложение 4) , описывает тенденцию уравнение параболы. Так как данное уравнение имеет наименьшее среднеквадратическое отклонение 1,78473 ц/га и, как правило , наименьший коэффициент вариации, который составил 11,6951 %.
На основе сделанных выводов рассмотрим прогнозные значения урожайности на ближайшие 3 года.
Таблица 9 Прогнозные значения урожайности подсолнечника.
| Годы | Прогнозные значения урожайности подсолнечника,ц/га | |||
| По уравнению прямой | По уравнению параболы | По уравнению экспоненты | По уравнению S-кривой | |
| 20,0158 | 24,2426 | 19,8240 | 16,3794 | |
| 20,7836 | 27,5465 | 20,7385 | 16,4035 | |
| 21,5515 | 31,3115 | 21,6951 | 16,4236 |
Так как уравнение параболы наиболее точно описывают тенденцию ряда динамики, то и прогноз данного уравнения получился наиболее высокий.
При составлении бизнес-плана исследуемому предприятию рекомендуем ориентироваться на показатели уравнения параболы, так как прогнозная урожайность через 3 года составит 31,3115 ц/га.
Дата добавления: 2015-01-19; просмотров: 294; Мы поможем в написании вашей работы!; Нарушение авторских прав |