КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зубчатых колес
| Диаметр заготов к, мм | Предел прочности, бв, МПа | Предел текучести, бе, МПа | Твердость, НВ, средн. | Термообработка |
| до 90 | Улучшение | |||
| свыше 120 | Улучшение |
Для шестерни:
материал – сталь 45,
термообработка – улучшение,
твердость НВ1 = 230.
Для колеса:
материал – сталь 45,
термообработка – улучшение,
твердость на 30 единиц ниже, чем у шестерни НВ2 = 200.
Допускаемые контактные напряжения
, (2.12)
где КHL – коэффициент долговечности. Если число циклов нагружения каждого зуба колеса больше базового, что имеет место при длительной эксплуатации редуктора, принимают КHL = 1;
[SH] – коэффициент безопасности для колес из нормализованной и улучшенной стали, а также при объемной закалке берут от 1,1 до 1,2. Принимаем [SH] = 1,1;
σн lim b – предел контактной выносливости при базовом числе циклов (табл. 2.5).
Таблица 2.5
| Предел контактной выносливости при базовом исле циклов | |||
| Способ термической обработки зубьев | Средняя твердость поверхности зубьев | Сталь | Предел контактной выносливости σH limb, МПа |
| Улучшение | НВ <350 (200, 230) | Углеродистая | 2 НВ + 70 |
Для углеродистых сталей с твердостью поверхности зубьев менее НВ350 (имеем НВ200) и термической обработкой улучшением выбираем по табл. 2.5 σн lim b = 2НВ+70.
Для шестерни
, (2.13)
где НВ1 = 230 – твердость поверхности зубьев;
КНL = 1 – коэффициент долговечности;
[SH] = 1,1 – коэффициент безопасности, тогда
Для колеса 
, (2.14)
где НВ2 = 200 – твердость поверхности зубьев у колеса;
КНL = 1 – коэффициент долговечности;
[SH] = 1,1 – коэффициент безопасности, тогда
Расчетное контактное допускаемое напряжение
[σН] = 0,45·([σН1]+ [σН2]), (2.15)
где [σН1] и [σН2] – допускаемые контактные напряжения соответственно для шестерни и колеса [см. формулы (2.13), (2.14)], тогда
[σН] = 0,45(482+427) ≈ 409 МПа.
Проверка. После определения [σН1], [σН2] следует проверить выполнение условия [σН]≤1,23[σН min], где [σН min] = [σН2], т.к. берём наименьшее значение из [σН2] и [σН1], следовательно [σН] ≤1,23·[σН2] или 409 ≤1,23·427 ≈ 525 МПа,
409 МПа < 525 МПа.
Требуемое условие выполнено.
Межосевое расстояниерассчитывается из условия контактной выносливости активных поверхностей зубьев
, (2.16)
где Ка = 43 – коэффициент для косозубых и шевронных колес ([1], с.32);
u = uред = 5 – передаточное число редуктора (см. выше);
Т2 = 605 ·103 Н·мм – вращающий момент на валу колеса [см. формулу (2.11)];
[σн] = 409 МПа – допускаемое контактное напряжение для косозубых колес [см. формулу (2.15)];
При проектировании редукторов обычно задаются коэффициентом ширины зубчатого венца по межосевому расстоянию 
, где b – ширина венца; 
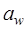– межосевое расстояние.
Для косозубых колес коэффициент ширины венца по межосевому расстоянию 
= 0,25÷0,63 ([1], с. 36). Принимаем 
= 0,4.
Коэффициент КHβ, учитывающий неравномерность распределения нагрузки по ширине венца, несмотря на симметричное расположение колес относительно опор, принимается предварительно как в случае несимметричного расположения колёс при твердости поверхности зубьев НВ ≤ 350 по табл. 2.6, т.к. со стороны цепной передачи действуют силы, вызывающие дополни 
тельную деформацию ведомого вала и ухудшающие контакт зубьев. Тогда принимаем коэффициент КHβ = 1,25. Принято наибольшее из значений, т.к. коэффициент ширины венца по диаметру (см. прим. к табл. 2.6).
ybd = b/d1 = 0,5yba(u + 1) =0,5∙0,4(5+1) = 1,2 > 0,8.
Тогда 
Ближайшее значение межосевого расстояния берем по ГОСТ 2185–66.
1-й ряд: 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500;
2-й ряд: 71, 90, 112, 140, 180, 224, 280, 355, 450, 560, 710, 900, 1120, 1400, 1800, 2240.
Предпочтителен первый ряд: аw = 200 мм.
Таблица 2.6
| Ориентировочные значения коэффициента KHb для зубчатых передач редукторов работающих п и перемен ой нагрузке | ||
| Расположение зубчатых колес относительно опор | Твердость (HB) поверхностей зубьев | |
| ≤ 350 (200;230) | > 350 | |
| Несимметричное | 1,10-1,25 (1,1) |
Примечание. Меньшие значения принимают для передач с отношением ybd = b/d1 = 0,4; при увеличении ybd до 0,6 для консольно расположенных ко
лес и ybd до 0,8 при несимметричном расположении их следует принимать большие из указанных в таблице значений KHb. При постоянной нагрузке KHb = 1.1
Нормальный модуль зацепленияпринимаем по следующей рекомендации: mn = (0,01÷0,02)· аw , (2.17)
где аw = 200 мм – межосевое расстояние;
mn = (0,01÷0,02)· 200 = 2 ÷ 4 мм.
Выбираем по ГОСТ 9563–60:
1-й ряд: 1; 1,25; 2; 2,5; 3; 4; 6; 8; 10; 12; 16; 20;
2-й ряд: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 7; 9; 11; 14; 18; 22.
Примем mn = 2,5 мм (предпочтителен 1-й ряд).
Угол наклона зубьев для косозубых колес может иметь значение β = 8 ÷ 15°. Примем предварительно β = 10о.
Определим числа зубьев шестерни и колеса.
Для шестерни
, (2.18)
где аw = 200 мм – межосевое расстояние [см. формулу (2.16)];
cos β = cos 10° = 0,985 – косинус угла наклона зубьев (см. выше);
u = uред = 5 – передаточное число редуктора (см. выше);
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)],
тогда
.
Округлим до целого числа Z1 = 26 .
Число зубьев колеса
Z2 = Z1·u, (2.19)
где Z1 = 26 – число зубьев шестерни [см. формулу (2.18)];
u = uред = 5 – передаточное отношение редуктора (см. выше),
тогда Z2 = 26·5 = 130.
Уточненное значение угла наклона зубьев
, (2.20)
где Z2 = 130 – число зубьев колеса [см. формулу (2.19)];
Z1 = 26 – число зубьев шестерни[см. формулу (2.18)];
аw = 200 мм – межосевое расстояние [см. формулу (2.16)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)],
тогда
β = 12 ° 50 /.
Примечание. Для косозубой передачи 8º < β < 15º. Если получается, что cos β ≥ 1, или β < 8º, или β > 15º, то применяют метод подбора: изменяют в допустимых пределах (2.17) модуль зацепления, выбирая его значение из ГОСТ 9563–60, или принимают другое значение межосевого расстояния из ГОСТ 2185–66 [обычно больше вычисленного по формуле (2.16)].
Дата добавления: 2014-10-31; просмотров: 151; Мы поможем в написании вашей работы!; Нарушение авторских прав |