
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Окружная сила
 , (2.33)
, (2.33)
где Т1 = 121 ·103 Н·мм – вращающий момент на ведущем валу редуктора [см. формулу (2. 10)];
d1 = 66,67 мм – делительный диаметр шестерни [см. формулу (2.21
тогда
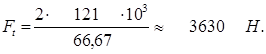
Радиальная сила:
 , (2.34)
, (2.34)
где Ft = 3630 Н – окружная сила [см. формулу (2.33)];
tg α = tg 20° = 0,36 (α – угол зацепления по ГОСТ 13755-81);
cosβ= 0,975 – косинус угла наклона зубьев [см. формулу (2.20)],
тогда
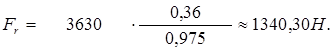
Осевая сила: Fα = Ft·tgβ, (2.35)
где tg β = tg 12 ° 50 / = 0,221 – тангенс угла наклона зубьев [см. формулу (2.20)];
Ft = 3630 Н – окружная сила [см. формулу (2.33)], тогда
Fα = 3630 · 0,221 ≈ 802 Н.
Проверяем зубья на выносливость по напряжениям изгиба по формуле
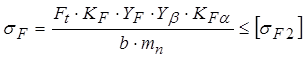 , (2.36)
, (2.36)
где Ft = 3630 Н – окружная сила [см. формулу (2.33)];
b2 = 80 мм – ширина колеса [см. формулу (2.27)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)];
КF = KFβ·KFυ – коэффициент нагрузки.
 КFβ учитывает неравномерность распределения нагрузки по длине зуба – это коэффициент концентрации нагрузки. Определяется по табл. 2.10 при ψbd = 1,275 [см. формулу (2.29)] и несимметричном расположении колес относительно опор.
КFβ учитывает неравномерность распределения нагрузки по длине зуба – это коэффициент концентрации нагрузки. Определяется по табл. 2.10 при ψbd = 1,275 [см. формулу (2.29)] и несимметричном расположении колес относительно опор.
Таблица 2.10
Значения коэффициента КFB при HВ <350
| Ψbd=b1/d1 | Расположение колес передачи относительно опор | |
| симметричное | несимметричное | |
| Ψbd1 = 1,2 | КFβ1 =1,33 | |
| Ψbd = 1,275 | КFβ - расчёт | |
| Ψbd2 = 1,4 | КFβ2 =1,38 |
Значение ψbd = 1,275 не совпадает с табличными значениями, поэтому для отыскания соответствующего ему значения КFβ применили формулу линейной интерполяции:
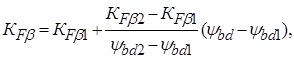
где ψbd1 = 1,2 ; ψbd2= 1,4 ; КFβ1 = 1,3 ; КFβ2 = 1,38 .
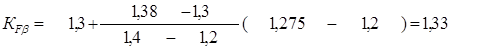
КFV – это коэффициент динамичности, выбираем по табл. 2.11, учитывая степень точности 8, твердость рабочей поверхности зубьев НВ≤350 и окружную скорость V = 3,4 м/с, получим КFV= 1,3 .
Таким образом, КF = 1,33 · 1,3 ≈ 1,73 .
Таблица 2.11
| Ориентировочные значения коэффициента КFV | ||||
| Степень точнос и | Твердость рабочей поверхности зубьев, НВ | Окружная скорость V, м/с | ||
| до 3 | 3-8 (3,4) | 8–12, | ||
 <350
(200;230) <350
(200;230)
| 1,3 | |||
 YF – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев ZV, определяется по табл. 2.12.
YF – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев ZV, определяется по табл. 2.12.
Для шестерни
 , (2.37)
, (2.37)
где Z1 = 26 – число зубьев шестерни [см. формулу (2.18)];
cosβ = 0,975 – косинус угла наклона зубьев [см. формулу (2.20)],
тогда
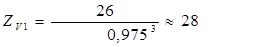 .
.
Для колеса
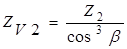 , (2.38)
, (2.38)
где Z2 = 130 – число зубьев шестерни [см. формулу (2.19)];
cosβ = 0,975 – косинус угла наклона зубьев [см. формулу (2.20)],
тогда 
Таблица 2.12
| Коэффициент, учитывающий форм зуба | |||||||||||
| Число зубьев, ZV |  25 25
| 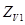 28 28
|  30 30
| 100 и более | |||||||
| Значение коэффициента YF | 4,28 | 4, |  3,90 3,90
|  3,84 3,84
|  3,80 3,80
| 3,70 | 3,66 | 3,62 | 3,61 | 3,6 | 3,60 |
Для шестерни число зубьев ZV1= 28 не совпадает с табличным значением, поэтому применим формулу линейной интерполяции
 ,
,
где



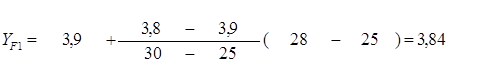
Для колеса: при ZV2= 140; YF2= 3,6.
Допускаемое напряжение находим по формуле
 , (2.39)
, (2.39)
где  – предел выносливости при эквивалентном числе циклов (табл. 2.13). Для стали 45 улучшенной при твердости НВ≤350
– предел выносливости при эквивалентном числе циклов (табл. 2.13). Для стали 45 улучшенной при твердости НВ≤350  =1,8 HВ;
=1,8 HВ;
[SF] – коэффициент безопасности.
Таблица 2.13
Значение предела выносливости при нулевом цикле изгиба  и коэффициента [SF]/ и коэффициента [SF]/
| ||||
| Марка стали | Термическая или термохимическая обработка | Твердость зубьев |  ,
МПа ,
МПа
| [SF]/ |
| Ст. 45 | Улучшение | НВ 180-350 | 1,8 НВ | 1,75 |
Предел выносливости:
для шестерни
 , (2.40)
, (2.40)
где НВ1= 230 – твердость материала (см. табл. 2.4), тогда
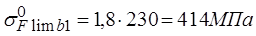 ;
;
для колеса
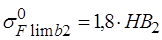 , (2.41)
, (2.41)
где НВ2 = 200 – твердость материала (см. табл. 2.4), тогда
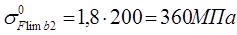 .
.
Коэффициент безопасности
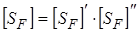 , (2.42)
, (2.42)
где 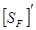 = 1,75 – учитывает нестабильность свойств материала зубчатых колес, его значение приведено в табл. 2.13;
= 1,75 – учитывает нестабильность свойств материала зубчатых колес, его значение приведено в табл. 2.13;
 – учитывает способ получения заготовки зубчатого колеса: для поковок и штамповок
– учитывает способ получения заготовки зубчатого колеса: для поковок и штамповок  =1.
=1.

 Допускаемые напряжения.
Допускаемые напряжения.
Для шестерни
 , (2.43)
, (2.43)
где  = 414 МПа – предел выносливости при эквивалентном числе циклов [см. формулу (2.40)];
= 414 МПа – предел выносливости при эквивалентном числе циклов [см. формулу (2.40)];
[SF]=1,75 – коэффициент безопасности [см. формулу (2.42)];
тогда 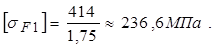
Для колеса 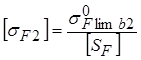 , (2.44)
, (2.44)
где 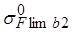 =360 МПа – предел выносливости при эквивалентном числе циклов [см. формулу (2.41)];
=360 МПа – предел выносливости при эквивалентном числе циклов [см. формулу (2.41)];
[SF] = 1,75 – коэффициент безопасности [см. формулу (2.42)], тогда
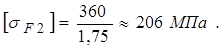
Проверку на изгибную выносливостьпроводим для того зубчатого колеса, для которого отношение 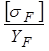 меньше. (2.45)
меньше. (2.45)
Для шестерни  , (2.46)
, (2.46)
где  = 237 МПа – допускаемое напряжение [см. формулу (2.43)]
= 237 МПа – допускаемое напряжение [см. формулу (2.43)]
YF1 =3,84 – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев (см. табл. 2.12), тогда
 .
.
Для колеса 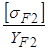 , (2.47)
, (2.47)
где 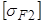 = 206 МПа – допускаемое напряжение [см. формулу (2.44)].
= 206 МПа – допускаемое напряжение [см. формулу (2.44)].
YF2 =3,60 – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев (см. табл. 2.12),тогда

Мы видим, что 62 МПа >57,2 МПа, таким образом, 
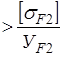 .
.
Следовательно, дальнейший расчет следует вести для зубьев колеса, т.к. вычисленное для него отношение меньше, чем для шестерни. Таким образом, берем YF = 3,6 (см. табл. 2.12).
Определяем коэффициент Yβ.Он введен для компенсации погрешности той же расчетной схемы зуба, что и в случае прямого зуба
 , (2.48)
, (2.48)
где β˚=12˚50′=12,83˚ – угол наклона делительной линии зуба [см. формулу (2.20)], тогда
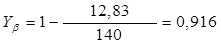 .
.
Определяем коэффициент 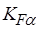 , учитывающий неравномерность распределения нагрузки между зубьями:
, учитывающий неравномерность распределения нагрузки между зубьями:
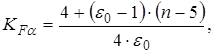 (2.49)
(2.49)
где  =1,5 – при учебном проектировании можно принимать среднее значение коэффициента торцового перекрытия;
=1,5 – при учебном проектировании можно принимать среднее значение коэффициента торцового перекрытия;
n = 8 – степень точности зубчатых колес, тогда
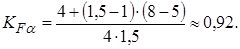
Проверяем прочность зуба колеса по формуле 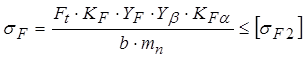 ,
,
где Ft = 3630 Н – окружная сила [см. формулу (2.33)];
b2 = 80 мм – ширина колеса [см. формулу (2.27)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)];
КF = 1,73 – коэффициент нагрузки;
YF = YF2 = 3,6 – коэффициент, учитывающий форму зуба(см.таблицу 2.12);
Yβ = 0,916 – компенсирует погрешности расчетной схемы зуба(см. формула 2.48);
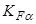 =0,92 –коэффициент, учитывающий неравномерность распределения нагрузки между зубьями (см. формулу 2.49);
=0,92 –коэффициент, учитывающий неравномерность распределения нагрузки между зубьями (см. формулу 2.49);
[σF] = 206 МПа – допускаемое напряжение для колеса [см. формулу (2. 44)], тогда
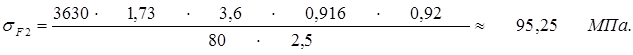
 95,25 МПа < 206 МПа. Условие прочности выполнено.
95,25 МПа < 206 МПа. Условие прочности выполнено.
Дата добавления: 2014-10-31; просмотров: 1465; Мы поможем в написании вашей работы!; Нарушение авторских прав |