
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение дифференциальноых уравнений математической модели системы без гасителя
Преобразуем математичесскую модель (6). Сгрупируем значения при yи φ. Разделим первое уравнения на массу, второе на момент инерции.
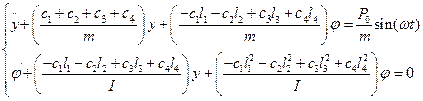 (7)
(7)
Для удобства дальнейших преобразований введем обозначения:
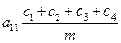

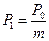 (8)
(8)

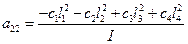
С учетом обозначений уравнения математической модели примут вид:
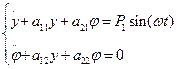 (9)
(9)
Решения уравнений будем искать в виде:
 (10)
(10)
где А1, А2 – амплитуды колебаний.
Подставив решение (10) в дифференциальные уравнения (9) получим следующую систему алгебраических уравнений для определения амплитуд колебаний А1 и А2.
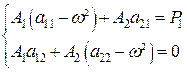 (11)
(11)
Отсюда находим:
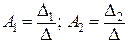 (12)
(12)
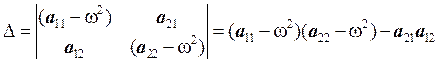 (13)
(13)
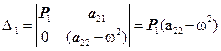 (14)
(14)
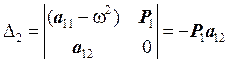 (15)
(15)
После вычисления определителей получим следующие формулы для амплитуд:
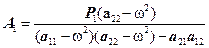 (16)
(16)
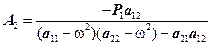 (17)
(17)
Построим амплитудно-частотные характеристики и зависимости углового и линейного перемещения от времени. Для этого разработана программа в программной среде MATLAB (приложение А).
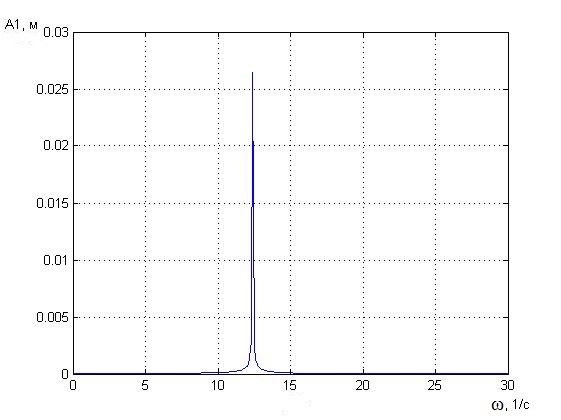
Рисунок 2.1 - Амплитудно-частотная характеристика линейных колебаний
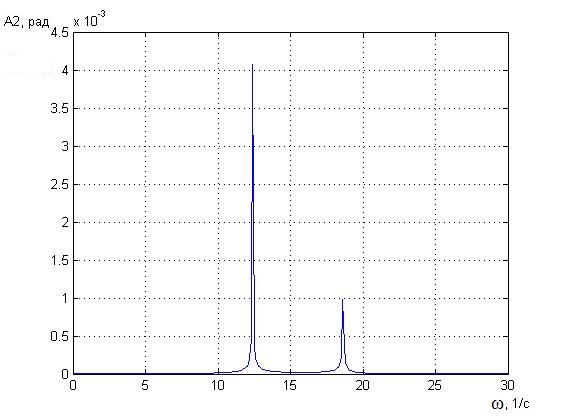
Рисунок 2.2 - Амплитудно-частотная характеристика угловых колебаний
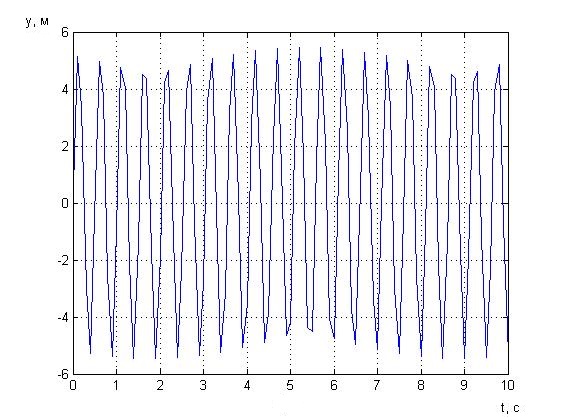
Рисунок 2.3 - Зависимость линейного перемещения от времени
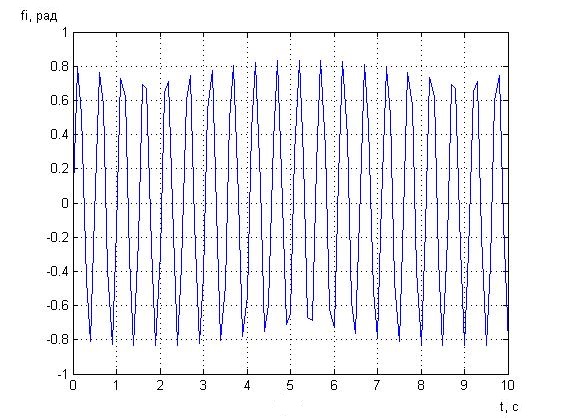
Рисунок 2.4 - Зависимость углового перемещения от времени
Условие
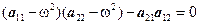 (18)
(18)
определяет собственные частоты рассматриваемой системы. При выполнении условия амплитуды А1 и А2 стремятся к бесконечности.
Определим собственные частоты системы. Преобразуем условие
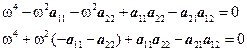 (19)
(19)
Корни уравнения и будут являться собственными частотами. Решим уравнение с помощью программной среды MATLAB (приложение Б). Результаты расчета:
k = -18.6279
-12.3900
18.6279
12.3900
Нас интересуют только положительные корни. При этих частотах и будет возникать резонанс, который видно на рисунках 2.1 и 2.2.
Дата добавления: 2015-01-19; просмотров: 201; Мы поможем в написании вашей работы!; Нарушение авторских прав |