Статический расчет системы виброизоляции

Статический расчет системы виброизоляции заключается в вычислении статических реакций и статических деформаций виброизоляторов с целью их правильной установки под оборудованием. В ходе статического расчета необходимо выявить положение объекта, который установлен на упругом подвесе, образованном совокупностью виброизоляторов.

Введем неподвижную систему координат ОXY (рисунок 1.1), проходящую через центр тяжести объекта в установочном положении. Под действием силы тяжести Р, виброизоляторы жесткости с₁ и с₂ деформируются на величины и соответственно. При этом возникают реакции в опорах, определяемые выражением:

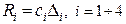(31)

Деформации можно определить с учетом вертикального перемещения объекта на величину у и возможного поворота на малый угол :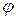

(32)

Для определения деформаций используем уравнения статического равновесия, представляющие собой сумму проекций действующих сил на ось у и сумму моментов сил, относительно точки О (рисунок 1.1) :

(33)

Подставив в выражения реакции опор с учетом деформации, после преобразований получим:

(34)

Решим систему с помощью программной среде MATLAB (Приложение Г). Результатом расчета является высота компенсирующих прокладок под соответствующие виброизоляторы

h1 = 0.0122 мм; h2 = 0.0096 мм; h3 = 0.0027 мм.

Рисунок 4.1 - Выравнивание объекта:

а – определение величины компенсирующей прокладки,

б – результат выравнивания

Заключение

В курсовой работе была рассмотрена система с двумя степенями свободы. Исследована динамика системы, составлена математическая модель системы с гасителем и без. На основе полученных математической модели системы без гасителя построены амплитудно-частотные характеристики и зависимости перемещения от времени, определены собственные частоты системы на которых виден резонанс. Выбрана частота гашения колебаний . Выбраны параметры гасителя , , рассчитана жесткость упругого элемента гасителя ю По полученным данным и математической модели с гасителем построены амплитудно-частотные характеристики и зависимости перемещения от времени, на рисунке 3.2 виден антирезонанс, на рисунке 3.5 видны потухшие колебания. Был выполнен статический расчет системы, рассчитаны компенсирующие прокладки под упругие элементы системы. Все расчеты были выполнены в программной среде MATLAB.

Список литературы

1. Методические указания по выполнению курсовых проектов (работ) по дисциплинам "Расчет и конструирование типовых узлов машин", "Динамика узлов и механизмов машин" / сост. Н.М. Бабкина, И.М. Беспалова, Н.А. Гренишина, Л.С. Мазин, В.К. Поляков. – СПб.: СПГУТД, 2009. – 29 с.

2. Вульфсон, И.И. Колебания в машинах / И.И. Вульфсон. – 2-е изд. – СПб. : СПГУТД, 2008. – 260 с.

3. Яблонский, А.А. Курс теоретической механики / А.А. Яблонский, В.М. Никифорова. – 16-е изд. – М.: КноРус, 2011. – 603 с.

ПриложениеА

Программа для построим амплитудно-частотные характеристики и зависимости углового и линейного перемещения от времени, для модели без гасителя.

m = 900;

c1 = 50000;

c2 = 20000;

c3 = 30000;

c4 = 40000;

P0 = 6;

P1 = P0/m;

l1 = 1.2;

l2 = 0.7;

l3 = 0.6;

l4 = 1.1;

h = 0.4;

I = 1/12*m*((l1+l4)^2+h^2);

i=1;

for w = 0:0.1:30

a11 = (c1+c2+c3+c4)/m; a12 = (-c1*l1-c2*l2+c3*l3+c4*l4)/m;

a21 = (-c1*l1-c2*l2+c3*l3+c4*l4)/I; a22 = (c1*l1^2+c2*l2^2+c3*l3^2+c4*l4^2)/I;

d = [ (a11-w^2) a12 ;...

a21 (a22-w^2) ];...

d1 = [ P1 a12 ;...

0 (a22-w^2) ];...

d2 = [ (a11-w^2) P1 ;...

a21 0 ];...

A1(i) = abs(det(d1)/det(d));

A2(i) = abs(det(d2)/det(d));

i=i+1;

end

w = 0:0.1:30;

figure(1)

plot(w,A1),grid, xlabel('w, 1/c'), ylabel('A1, м')

figure(2)

plot(w,A2),grid, xlabel('w, 1/c'), ylabel('А2, рад')

w = 12.39;

t = 0:0.1:10;

d = [ (a11-w^2) a12 ;...

a21 (a22-w^2) ];...

d1 = [ P1 a12 ;...

0 (a22-w^2) ];...

d2 = [ (a11-w^2) P1 ;...

a21 0 ];...

A1 = abs(det(d1)/det(d));

A2 = abs(det(d2)/det(d));

y = A1.*sin(w.*t);

fi = A2.*sin(w.*t);

figure(4)

plot(t,y), grid, xlabel('t, c'), ylabel('y, м')

figure(5)

plot(t,fi), grid, xlabel('t, c'), ylabel('fi, рад')