Решение дифференциальноых уравнений математической модели системы с гасителем

Преобразуем математичесскую модель (5). Сгрупируем значения при y и φ. Разделим первое уравнения на массу, второе на момент инерции, третье на массу гасителя.

(20)

Для удобства дальнейших преобразований введем обозначения:

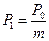
(21)

С учетом обозначений уравнения математической модели примут вид:

(22)

Решения уравнений будем искать в виде:

(23)

где А₁, А₂ – амплитуды колебаний.

Подставив решение (23) в дифференциальные уравнения (22) получим следующую систему алгебраических уравнений для определения амплитуд колебаний А₁, А₂,А₃.

(24)

Отсюда находим:

(25)

(26)

(27)

(28)

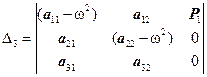(29)

Определим параметры динамического гасителя. - масса гасителя, 0,1 от массы системы. . - расстояние от точки О до гасителя, выберем равной . - жесткость пружины гасителя, определяется из уравнения амплитуды, при условии, что . Приравняем к 0, подставим обозначения (21), выразим :

(30)

- частота гашения, выберем

Построим амплитудно-частотные характеристики и зависимости углового и линейного перемещения от времени. Для этого разработана программа в программной среде MATLAB (приложение B). В результате расчета, на рисунке 3.2 виден антирезонанс на частоте гашения , на рисунке 3.5 видны погашенные колебания.

Рисунок 3.1 - Амплитудно-частотная характеристика линейных колебаний

Рисунок 3.2 - Амплитудно-частотная характеристика угловых колебаний

Рисунок 3.3 - Амплитудно-частотная характеристика гасителя

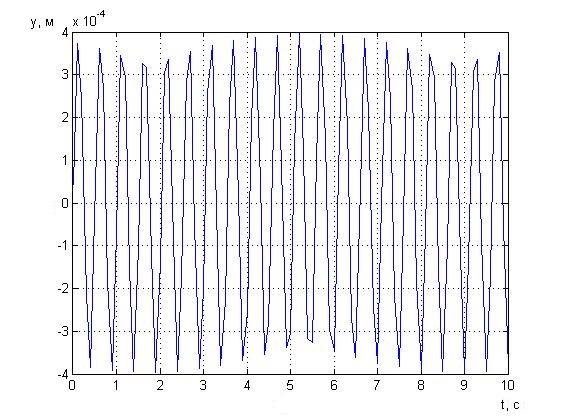
Рисунок 3.4 - Зависимость линейного перемещения от времени

Рисунок 3.5 - Зависимость углового перемещения от времени

Рисунок 3.6 - Зависимость перемещения гасителя от времени