Глобальная формула Тейлора с остаточным членом различного вида.

Ответ:

Формула Тейлора.

Тейлор (1685-1731) – английский математик

Теорема Тейлора. 1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но х ¹ а.

Тогда между точками х и а найдется такая точка e, что справедлива формула:

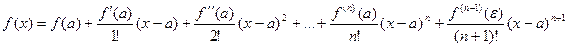
- это выражение называется формулой Тейлора, а выражение:

называется остаточным членом в форме Лагранжа.

Доказательство. Представим функцию f(x) в виде некоторого многочлена P_n(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.

(1)

Многочлен P_n(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию.

Представим этот многочлен с неопределенными пока коэффициентами:

(2)

Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений:

(3)

Решение этой системы при х = а не вызывает затруднений, получаем:

…………………….

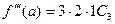
Подставляя полученные значения C_i в формулу (2), получаем:

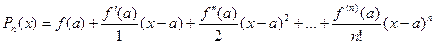
Как было замечено выше, многочлен не точно совпадает с функцией f(x), т.е. отличается от нее на некоторую величину. Обозначим эту величину R_n+1(x). Тогда:

f(x) = P_n(x) + R_n+1(x)

Теорема доказана.