Выпуклость графика функций и точки перегиба.

Ответ:

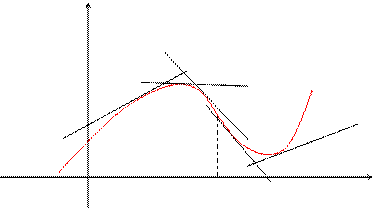
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

у

x

На рисунке показана иллюстрация приведенного выше определения.

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

Доказательство. Пусть х₀ Î (a, b). Проведем касательную к кривой в этой точке.

Уравнение кривой: y = f(x);

Уравнение касательной:

Следует доказать, что .

По теореме Лагранжа для f(x) – f(x₀): , x₀ < c < x.

По теореме Лагранжа для

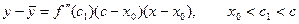
Пусть х > x₀ тогда x₀ < c₁ < c < x. Т.к. x – x₀ > 0 и c – x₀ > 0, и кроме того по условию

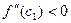, следовательно, .

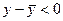Пусть x < x₀ тогда x < c < c₁ < x₀ и x – x₀ < 0, c – x₀ < 0, т.к. по условию то

.

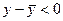Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

Теорема доказана.

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при

x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.

2) Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.

Теорема доказана.

29. Достаточное условие выпуклости графика функции и точки её перегиба.

Ответ:

Теорема. Для того, чтобы дважды дифференцируемая в точке x₀ функция была выпукла вверх (вниз) в этой точке, необходимо и достаточно, чтобы вторая производная этой функции в x₀ была неположительной (неотрицательной).
Доказательство. Пусть функция y = f ( x ) выпукла вниз в точке х₀. Разложим функцию в ряд Тейлора в данной точке х₀:

.

Следует отметить, что первые два слагаемых ряда Тейлора совпадают с правой частью уравнения касательной, проведённой в графику функции y = f (x) в точке х₀:

Y = f ( x₀ ) + f '( x₀ )·( x − x₀ ).

Учитывая, что слагаемое o(x - x₀)² в достаточно малой окрестности точки х₀ мало, и на знак выражения влияния не оказывает, получим зависимость знака второй производной на направление выпуклости

sign ( f ( x ) − Y) = sign ( f ''( x₀ ) ).

Теорема. Для того чтобы дважды дифференцируемая на интервале (а, b) функция, была выпукла вверх (вниз) в нем, необходимо, чтобы во всех точках этого интервала вторая производная функции была ≤ 0 ( ≥ 0).
Доказательство. Пусть функция в произвольной точке х₀ Î (a, b) выпукла вниз. Тогда в достаточно малой окрестности точки х₀ справедливо неравенство f ( x ) ≥ f ( x₀ ) + f ' ( x₀ )·( x - x₀ ).
Запишем последнее неравенство в виде

f ( x ) − f ( x₀ ) − f ' ( x₀ )·( x − x₀ ) ≥ 0.

Применяя формулу Лагранжа к первому и второму слагаемому, получим

[ f ' ( c₁ ) − f ' ( x₀ ) ]·( x − x₀ ) ≥ 0.

Применяя ещё раз формулу Лагранжа в квадратной скобке, получим

f '' ( c₂ )·( c₁ − x₀ )·( x − x₀ ) ≥ 0,

откуда непосредственно следует f '' ( c₂ ) ≥ 0 так как x₀ < с₂ < c₁ < x. Поскольку аргумент х выбран произвольно в достаточно малой окрестности точки х₀, то и аргумент для второй производной в этом случае тоже произволен в достаточно малой окрестности точки х₀.