Нахождение наименьшей высоты балки.

Определив расчетные усилия, переходим к нахождению наименьшей высоты балки из условия нормы жесткости F/L = 1 / 550 при сосредоточенных нагрузках Р. При определении требуемой высоты следует учесть, что по условию прогиб ограничен лишь в отношении нагрузки Р. Так как напряжение от суммарного момента МΣ=1248 кНм достигает [σ]Р, то напряжение от момента, вызванного сосредоточенными грузами МР=858 кНм, что будет составлять 0,8[σ]Р. Это напряжение следует брать вместо [σ]Р при определении требуемой высоты балки h.

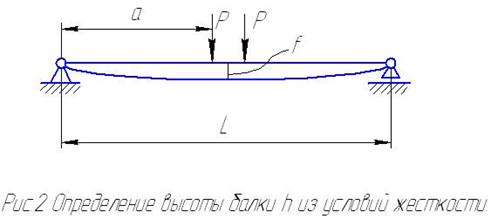
Прогиб балки от двух сосредоточенных сил Р, расположенных симметрично в пролете (рис.2):

Подставив значение Рα=М, получим:

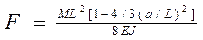Если выразить М через напряжение 0,8[σ]Р, вызванное сосредоточенными силами и умноженное на момент сопротивления W=2J/h, то получим:

откуда требуемая высота балки равна:

Чтобы определить требуемую высоту балки из условия ее наименьшего сечения, нужно задаться толщенной вертикального листа.

Примем SВ=15мм=1,5см.

Требуемая высота из условия наименьшей массы определяется по формуле:

Так как требуемая высота, найденная из условия нормы жесткости, больше, чем высота, найденная из условия наименьшей массы, то ее и следует принять в расчет при подборе сечения (рис.3).

Таким образом: высота балки h=148см;

толщена вертикального листа SВ=1,5см;

высота вертикального листа (примем) hВ=145см.