Принцип линейной деформируемости.

Грунты, как отмечалось ранее, представляют собой сложней­шие минерально-дисперсные образования, состоящие из разнооб­разных взаимно связанных частиц, обладающих различными меха­ническими свойствами.

Применение к грунтам общей теории напряжений, разработан­ной для сплошных упругих тел, требует особого рассмотрения. Так, в любых дисперсных телах внешняя нагрузка передастся от одной частицы к другой лишь через точки контакта частиц, кото­рые в большинстве случаев расположены незакономерно или по некоторой структурной сетке.

Определение напряжений в грунтах является значи­тельно более сложной задачей, чем в сплошных телах.

При действии внешней нагрузки отдельные фазы (компоненты) грунтов по-разному сопротивляются силовым воздействиям и по-разному деформируются, что является главнейшей особенностью напряженно-деформированного состояния грунтов.

При общем рассмотрении необходимо изучить напряженно-де­формированное состояние как грунта в целом, так и отдельных его фаз во взаимодействии между собой.

Кроме того, необходимо учи­тывать, что деформируемость не только грунта в целом, но и от­дельных его фаз (например, твердых частиц) зависит от времени действия нагрузки вследствие явления ползучести.

Рассмотрим общий случай зависимости относительной деформа­ции ε от величины нормального напряжения σ для грунта в целом. Такое рассмотрение будет полностью справедливо для начального и конечного состояний грунта, когда отсутствует перераспределе­ние фаз в единице объема (например, когда при уплотнении за­кончится выдавливание воды из пор грунта). При рассмотрении промежуточных состояний необходимо учитывать процесс консо­лидации, ползучесть скелета и пр.

При анализе зависимости деформаций от напряжений следует различать, по крайней мере, два вида грунтов: сыпучие и связные.

Для сыпучих грунтов при однократном загружении всегда воз­никают необратимые смешении и повороты зерен грунта относи­тельно друг друга, что обусловливает постоянное наличие остаточ­ных деформаций.

Для связных грунтов на характер деформирования существен­но влияют структурные связи, как жесткие, так и вязкие.

При жестких связях, если величина нагрузки такова, что при ее действии прочность связей не нарушается, грунт будет дефор­мироваться как квазнтвердое тело.

При вязких (водно-коллоидных) связях в грунтах некоторые связи начинают разрушаться (или вязко течь) уже при весьма небольших усилиях, другие—при несколько больших и т.д., что и обусловливает и у этих грунтов постоянное наличие при разгруз­ке не только обратимых, но и остаточных деформаций. Важно от­метить, что остаточные деформации часто во много раз превосхо­дят по величине деформации обратимые.

Природные связные грунты в большинстве случаев имеют и жесткие и часто вязкие связи различной прочности, поэтому про­цесс деформирования их является весьма сложным.

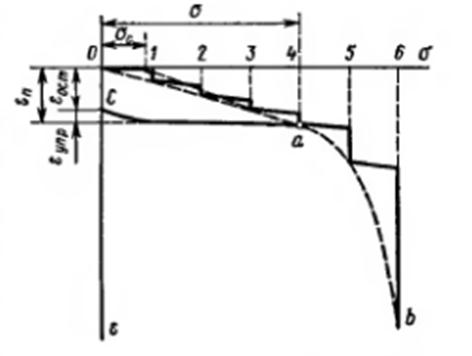
Рис. Зависимость между дефор­мациями е и нормальными напряже­ниями о для грунта при ступенчатом возрастании нагрузки

В самом общем случае, как показывают многочисленные исследования, зависимость между деформациями и напряжениями для грунтов, при значительных напряжениях, будет нелинейной (рис., пунктирная кривая Oab).

Эту зависимость в общем виде можно представить функцией

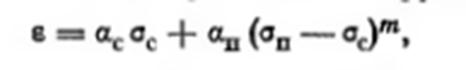(2.35)

где α_с и α_n – коэффициенты, определяемые опытом; σ_с – напряжение, не превосходящее начальной прочности структурных связей (σ_с<р_стр); (σ_п—σ_с)=σ – действующее нормальное напряжение, обусловливающее деформации грунта при частичном или полком нарушении структурных связей; m — параметр нелинейности, также определяемый опытным путем.

Можно принять, что коэффициент α_с обратно пропорционален модулю нормальной упругости Е, т.е. α_с = l/Е.

Что касается коэффициента α_n, то природа его значительно сложней. Если рассматривать только стабилизированные напряжения, то величина этого коэффициента будет зависеть от модуля общей деформации Е₀ грунт, который в об­щем случае может входить в выражение в некоторой степени r, меньшей или равной единице, а также от коэффициента β, оценивающего способность бокового расширения грунта, т. е. можно принять

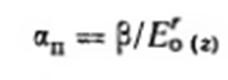
где параметр r≤1 также определяется опытным путем.

Если рассматривать деформации грунта при давлениях, больших структурной прочности сжатия, то зависимости (2.35) можно придать следующий вид:

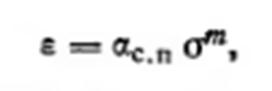(2.35')

где α_c,n — некоторый общий коэффициент пропорциональности, в простейшем случае равный

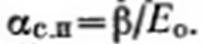
Общая зависимость (2.35') даже в представленной простой форме еще очень сложна для применения на практике.

При не очень больших изменениях внешних давлений (порядка 0.3—0,5 МПа, а для плотных и твердых грунтов и до 0,5—0,7 МПа) с достаточной для практических целей точностью зависимость между деформациями ε и напряжениями σ может приниматься линейной (см. спрямленный участок Оа на кривой рис.), что значительно упрощает расчеты и не вносит в них недопустимых погрешностей. Полагая в выражении (2.35) значение параметра m=1 (что вполне допустимо при величине напряжений, меньших практического предела пропорциональности), между общими деформациями и напряжением при постоянстве модуля обшей деформации будем иметь

(2.36)

т.е. при небольших изменениях напряжений к грунтам с полным к тому основанием можно применять теорию линейно деформируемых тел.

Зависимость между общими деформациями и напряжениями линейна, то для определения напряжений в грунтах полностью будут применимы решения теории упругости; для определения же общих деформаций грунтов необходимы добавочные условия (например, зависимость изменения коэффициента пористости от давления и др.).

Изложенное позволяет сформулировать для грунтов так называемый принцип линейной деформируемости, а именно:

При небольших изменениях давлений можно рассматривать грунты как линейно деформируемые тела, т.е. с достаточной для практических целей точностью можно принимать зависимость между общими дефорнациями и напряжениями для грунтов линейной.

Этот принцип вытекает также и из рассмотренного случая сжатия слоя грунта при сплошной нагрузке (компрессии грунта) в диапазоне давлений, при котором справедлив закон уплотнения. Действительно, по формуле (2.5')

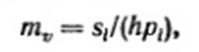
а так как относительная деформация

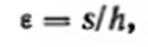
то

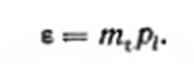(2.36^/)

Сравнивая далее выражение (2.36) с выражением (2.36^/) и принимая во внимание, что в рассматриваемом случае

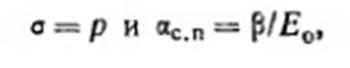
получим

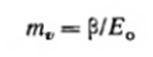(2.37)

или

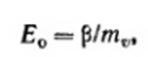(2.37^/)

где Е_о — модуль общей деформации грунта, определяемый по формуле (2.27),

используя результаты испытаний образцов грунта на трехосное сжатие или данные полевых опытов пробной нагрузкой.

Коэффициент β, как указывалось ранее, зависит от коэффициента относительной поперечной деформации грунта (аналогичного коэффициенту Пуассона для упругих тел) и приблизительно равен: для песков β – 0,8; для супесей β=0,7; для суглинков β=0,5 и для глин β=0,4.

Следует отметить, что принцип линейной деформируемости грунтов (справедливый для грунтов средней уплотненности при давлениях порядка 0,1—0,3 МПа и несколько более) является одним из основных в современной механике грунтов, так как на нем базируются почти все инженерные расчеты напряжений и деформаций естественных грунтовых оснований. Для слабых же грунтов (при несущей способности их меньше 0,1 МПа) необходимо исходить из нелинейной зависимости между деформациями и напряжениями.

Тема 9. Определение напряжений в массиве грунта. Распределение напряжений в случае пространственной задачи от действия одной или несколь­ких сосредоточенных сил, действие равномерно распределенной нагрузки; определение сжимающих напряжений по методу угловых точек; способ элементарного суммирования