
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Hешаем задачу
Пусть под действием силы Р точка М – переместилась в точку М1
S – перемещение т. М
Можно записать
S =A 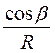 ; S1=A ; S1=A 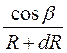
|
  cos 0° = 1 Smax R= 0 cos 0° = 1 Smax R= 0
  cos 90° = 0 Smin R= cos 90° = 0 Smin R= 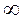 А – коэффициент пропорциональности
А – коэффициент пропорциональности
|
Относительное перемещение точки:



 еR =
еR = 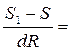
 =
= 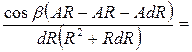

Согласно 1 постулата теории упругости между напряжениями и деформациями должна быть прямая зависимость, т.е.
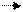
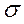 R = B еR =AB
R = B еR =AB 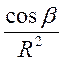 (1) В – коэффициент пропорциональности АВ ?
(1) В – коэффициент пропорциональности АВ ?
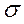 R – определяется как в сопромате («метод сечений» мысленно разрезают балку и оставшуюся часть уравновешивают).
R – определяется как в сопромате («метод сечений» мысленно разрезают балку и оставшуюся часть уравновешивают).
Для составления условия равновесия проведем через точку А полушаровое сечение с центром в точке приложения нагрузки.

Нормальное напряжение σ будет изменяться от 0 возле ограничивающей плоскости до max оси Z.
Условия равновесия заключается в том, что сумма проекций всех сил на вертикальную ось = 0.
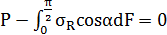 , где
, где
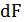 – поверхность элементарного шарового пояса.
– поверхность элементарного шарового пояса.
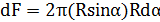 .
.
Подставив dF в условие равновесия и проинтегрировав в заданных пределах, получим:
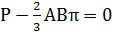 , где
, где
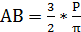 .
.
Подставим АB в формулу j:
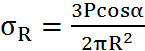 – формула Буссинеска.
– формула Буссинеска.
Из этой формулы можно получить сосредоточенные силы для пространственной задачи.
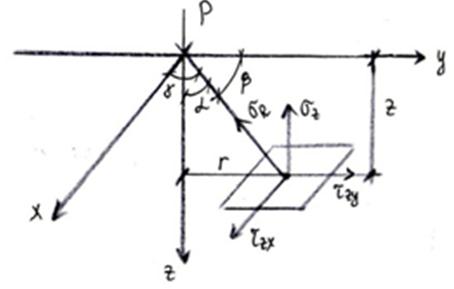
Отнесем величину радиальных напряжении не к площадке, перпендикулярной радиусу, а к площадке, параллельной ограничивающей плоскости и составляющей с ней угол α. Обозначим это напряжение σR'.
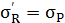 cosα,
cosα,
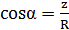 ,
,
 ,
,
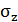 =
=  ,
, 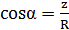 ,
,
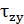 =
= 
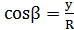 ,
,
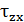 =
= 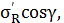
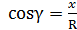 .
.
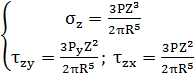 ,
,
Аналогичным образом выводятся выражения для 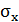 ,
, 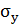 ,
,  ,
, 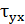 ,
, 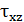 ,
, 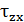 .
.
При расчете максимального выражения для определения 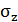 придают удобный вид, учитывая, что:
придают удобный вид, учитывая, что:
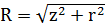 ,
,
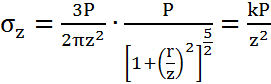 , где
, где
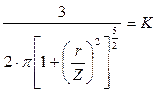
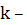 коэффициент, зависящий от отношения
коэффициент, зависящий от отношения  , и определяется по таблице.
, и определяется по таблице.
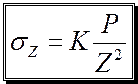 ; (*)
; (*)
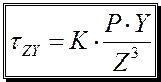 ;
;
Дата добавления: 2015-01-29; просмотров: 448; Мы поможем в написании вашей работы!; Нарушение авторских прав |