Следовательно, в расчётах механики грунтов, с учетом отмеченных допущений, можно использовать теорию упругости.

Следует также отметить, что уравнении теории линейно деформируемых тел будут справедливы лишь дли массива грунта при отсутствии в нем областей предельного напряженного состояния, для которых зависимость между деформациями и напряжениями нелинейна. При большом развитии областей предельного равновесия, например под сооружениями, несущими значительную нагрузку, близкую к предельной, применение решений теории линейно деформируемых тел будет неправомочным.

Распределение напряжений в случае пространственной задачи от действия одной или нескольких сосредоточенных сил, действие равномерно распределенной нагрузки; определение сжимающих напряжений по методу угловых точек; способ элементарного суммирования

Напряжение в грунтовом однородном полупространстве от внешних сосредоточенных сил

Для характеристики напряженного состояния грунтового массива используются следующие напряжения:

σ_z – вертикальное нормально напряжение;

, – горизонтальные нормальные напряжения, действующие в направлении осей OX и OY;

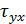, – касательные напряжения, действующие || OZ;

, – касательные напряжения, действующие || OY;

, – касательные напряжения, действующие || OX;

Определение напряжений в массиве грунта от сосредоточенной силы. (задача Буссинеско 1885 г.)

Рассмотрим действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости (рис. 3.1). Будем считать полупространство однородным в глубину и в стороны и линейно деформируемым.

Задача будет заключаться в определении всех составляющих напряжений: σ_z, σ_x, σ_y, τ_zy, τ_zx, τ_xy для любой точки полупространства, имеющей координаты z, у, х или R и β.

Р 0 R r M М1 Z

Определить значения вертикальных напряжений z и касательных напряжений; ; в точке М, расположенной на площадке параллельной плоскости ограничивающий массив.