
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 10. Распределение напряжений в случае плоской задачи: основные предпосылки; действие равномерно распределенной нагрузки; линии равных напряжений; главные напряжения
Определение напряжений в массиве грунта при плоской задаче.(Задача Фламана)
Условия плоской задачи будут иметь место в случае, когда напряжения распределяются в одной плоскости, в направлении же перпендикулярном они будут или равны нулю, или постоянны. Это условие имеет место для очень вытянутых в плане сооружений, например ленточных и стеновых фундаментов, оснований подпорных стенок, насыпей, дамб и подобных сооружений. Для этих сооружений в любом месте, за исключением лишь краевых участков (от края по длине примерно 2—3 ширины сооружения), распределение напряжений в любом проведенном сечении будет таким же, как и в других соседних, при условии, что в направлении, перпендикулярном рассматриваемой плоскости, нагрузка не меняется.
в                        Y
X Z
Y
X Z
| Определение напряжений в условиях плоской задачи значительно упрощается и во многих случаях может быть представлено в удобной форме. Вычисление составляющих напряжений:
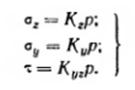
|
Значения коэффициентов влияния Кz, Ky, Kyz, приведены в таблице в зависимости от относительных координат z/b и y/b.
Линии равных напряжений
 |


|



 Р
Р
 |

|
 в
в 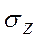 – определяется интерполяцией
– определяется интерполяцией



|




 изобары
изобары
горизонтальные сечения, в результате можно найти такую систему точек, в которых  равны – соединив их – получим линии равных напряжений (изобары).
равны – соединив их – получим линии равных напряжений (изобары).
Аналогичная картина - при разрезе луковицы. Поэтому часто линии равных напряжений (изобары) называют “луковицей напряжений”.
                      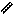  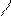      в в
Р
0,2 Р ,5 в
Z
| Определим  – линии равных горизонтальных напряжений «изохоры» (распоры). – линии равных горизонтальных напряжений «изохоры» (распоры).
Распоры | ||||||||||||||||||
| Линии равных напряжений касательных напряжений t(сдвиги) | |||||||||||||||||||
 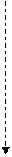  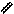     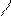      в в
2 в
|
Для расчета осадок фундаментов необходимо знать эпюру  - по вертикальным сечениям массива грунта.
- по вертикальным сечениям массива грунта.
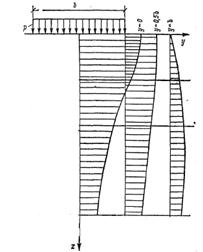
Рис. 6.7. Эпюры напряжений σz, вертикальным (б) сечениям
Главные напряжения, т. е. наибольшие и наименьшие нормальные напряжения, будут для площадок, расположенных по вертикальной оси симметрии нагрузки.
Можно показать, что главными площадками будут также площадки, расположенные по биссектрисам углов видимости и площадкам, им перпендикулярным.
Значения главных напряжений получим:
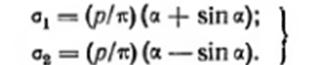 (3.12)
(3.12)
α-угол видимости
Формулы (3.12) весьма часто применяют при оценке напряженного состояния в основаниях сооружений, особенно предельного.
Они дают также возможность построить эллипсы напряжений для различных точек напряженного линейно деформируемого полупространства (рис. 3.12), наглядно иллюстрирующих изменение напряжений в грунте под полосообразной нагрузкой.
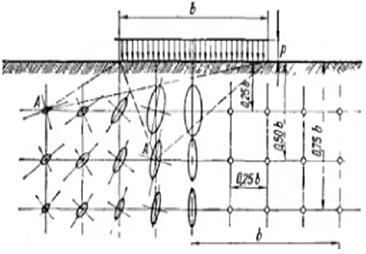
Рис 3.12. Эллипсы напряжений при действии равномерно распределенной нагрузки в условиях плоской задачи
Тема 11. Распределение давления по подошве фундаментов – контактная задача: контактные давления; эпюры; распределение сжимающих напряжений в слое грунта ограниченной толщины на несжимаемом основании, распределение напряжений от собственного веса грунта
Распределение напряжений на подошве фундамента (Контактная задача)
Этот вопрос имеет особое значение для гибких фундаментов, рассчитываемых на изгиб.
|
















 Если известно Рконт, то загружая этой величиной фундамент, можно легко определять усилия в конструкции тела фундамента.
Если известно Рконт, то загружая этой величиной фундамент, можно легко определять усилия в конструкции тела фундамента.












 Из курса сопротивления материалов известно, что напряжения для сжатых конструкций определяются по обобщенной формуле:
Из курса сопротивления материалов известно, что напряжения для сжатых конструкций определяются по обобщенной формуле:
|
 smax, min =
smax, min = 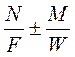 - но здесь не учитывается работа сжимаемого основания.
- но здесь не учитывается работа сжимаемого основания.
Теоретические исследования по этому вопросу провел Буссинеcка для жесткого круглого штампа:
|















 Рr=
Рr=  ;
;
 |  | ||
 При r = r ® Рr = ¥
При r = r ® Рr = ¥
 При r = 0 ® Рr = 0,5Рср
При r = 0 ® Рr = 0,5Рср
















 Фактически, грунт под подошвой фундамента, разрушаясь, приводит к перераспределению напряжений, возникает практическая эпюра.
Фактически, грунт под подошвой фундамента, разрушаясь, приводит к перераспределению напряжений, возникает практическая эпюра.
 |  | ||||||||
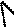 | |||||||||
| |||||||||
| |||||||||
Г » 10 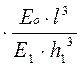 - гибкость фундамента
- гибкость фундамента
Ео – модуль деформации грунта
l – полудлина фундамента (балки)
Е1 – модуль упругости материала фундамента
h1 – высота фундамента
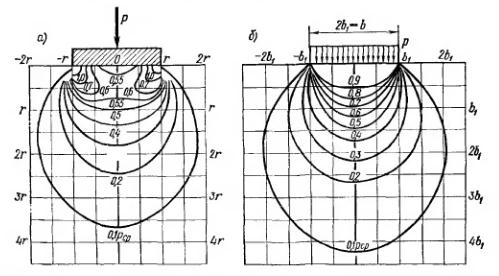
Рис. 3.19. Изобары в грунте под фундаментами абсолютно жестким (а) и гибким (б)
Концентрация давлений у края жестких фундаментов сказывается на распределении напряжений в массиве грунта лишь на небольшую глубину от подошвы, и общая "луковица" напряжений незначительно изменяется, вследствие чего общая осадка фундаментов мало зависит от их жесткости, хотя осадка абсолютно жестких фундаментов, несколько меньше, чем гибких.
На рис. 3.19 изобары для фундаментов абсолютно жесткого и абсолютно гибкого, которые подтверждают сказанное выше. Для подошвы фундаментов эпюра контактных давлений по решениям, излагаемым в курсе сопротивления материалов, будет прямолинейной — равномерной или трапецеидальной, тогда как по строгому решению теории упругости для абсолютно жестких фундаментов она всегда будет седлообразной; для фундаментов же конечной жесткости эпюра может принимать очертания от седлообразного до параболического (см. рис. 3.18, б).
Следует сказать, что распределение контактных давлений по подошве фундаментов зависит не только от гибкости фундаментов, но и от глубины их заложения, величины внешней нагрузки, обусловливающей развитие пластических деформаций в грунте, а следовательно, и от прочностных свойств грунта.
В заключение отметим, что материалы, изложенные в настоящем разделе, могут служить основой при разработке методов проектирования и расчета фундаментных балок и плит, лежащих на сжимаемом линейно деформируемом полупространстве.
В практике проектирования неоднородность основания учитывается в следующих случаях:
– слой сжимаемого грунта залегает на практически несжимаемом (например, скальном) основании;
– под сравнительно малосжимаемым слоем залегает более сжимаемый грунт.
На рис.5.12 приведены схематические эпюры вертикальных нормальных напряжений под центром прямоугольной площадки, загруженной равномерно распределенной нагрузкой при жестком (кривая 2) и слабом (кривая 3) подстилающих слоях. Кривая 1 показывает распределение напряжений в однородном основании. Как видно из рис. 5.12, при жестком подстилающем слое напряжения на границе слоев увеличиваются, а при слабом подстилающем слое уменьшаются.
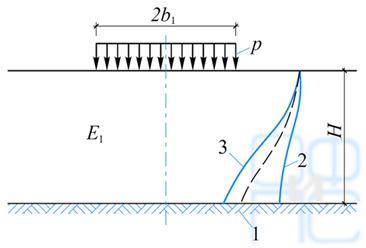
Рис. 5.12. Схема распределения вертикальных нормальных напряжений в основании под центром равномерно загруженной, прямоугольной площадки
1—однородном; 2—с жестким подстилающим слоем; 3—со слабым подстилающим слоем
Из рассмотрения эпюр распределения сжимающих напряжений (давлений) вытекает, что наличие жесткого несжимаемого слоя вызывает концентрацию (возрастание) напряжений по оси нагрузки, тогда как увеличение сжимаемости грунта с глубиной уменьшает концентрацию напряжений.
Дата добавления: 2015-01-29; просмотров: 968; Мы поможем в написании вашей работы!; Нарушение авторских прав |


 0,3 Р
0,3 Р
 0,1 Р
0,1 Р










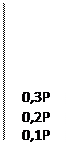
 Z
Z

