
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теория фильтрационной консолидации грунтов.
Процесс уплотнения грунта во времени, вследствие уменьшения влажности (пористости) при постоянном напряженном состоянии называется процессом консолидации
Предпосылки теории фильтрационной консолидации сводятся к следующему:
1 скелет грунта линейно-деформируемый, деформируется мгновенно после приложения к нему нагрузки и вязкими связями не обладает;
2 структурной прочностью грунт не обладает, давление в первый момент полностью передается на воду;
3 грунт полностью водонасыщен, вода и скелет объемно несжимаемы, вся вода в грунте гидравлически непрерывна;
4 фильтрация подчиняется закону Дарси.
Таким образом, рассматриваемая ниже теория фильтрационной консолидации грунтов (без дополнительных условий) будет применима для неуплотненных, полностью водонасыщенных (слабых) глинистых грунтов.
Отметим, что отдельными учеными в теорию фильтрационной консолидации введен ряд усовершенствований и дополнений, учитывающих свойства природных глинистых грунтов различной консистенции, и установлены пределы применимости отдельных решений.
Дифференциальное уравнение одномерной задачи теории фильтрационной консолидации позволяет сформулировать (при сделанных выше предпосылках) задачу о протекании во времени осадок полностью водонасыщенного слоя грунта при уплотнении его сплошной равномерно распределенной нагрузкой в условиях односторонней фильтрации воды, полагая, что изменение расхода выдавливаемой из пор грунта воды с достаточной точностью определяется законом фильтрации, а соответствующее изменение пористости — законом уплотнения.
Примем, что в начальный момент времени грунтовая масса находится в статическом состоянии, т. е. поровое давление воды равно нулю. Обозначим: pw— поровое давление сверх гидростатического в воде; рz — давление, передающееся на твердые частицы (эффективное).

Рис. 5.5. Схема распределения давлений в скелете грунта (pz) и в поровой воде (pw) в водонасыщенном слое при сплошной нагрузке для разных промежутков времени
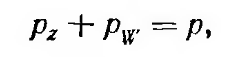
Для элементарного слоя dz на глубине z в грунтовой массе увеличение расхода воды q равно уменьшению пористости грунта n, т. е.

Коэффициентом консолидации грунта cv, т. е.
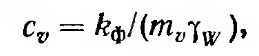
mν – коэффициент относительной сжимаемости грунта
Окончательно будем иметь
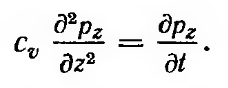 (5.12)
(5.12)
Для случая равномерного (в стабилизированном состоянии) распределения уплотняющих давлений по глубине решение уравнения (5.12) может быть представлено в виде
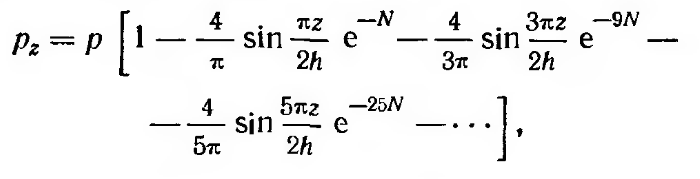
где
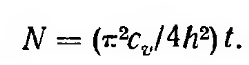
Наибольшее, однако, значение для практики имеет формула осадки слоя грунта при сплошной нагрузке для любого промежутка времени от начала загружения, т. е. осадка st.
Для определения этой величины введем понятие о степени консолидации (уплотнения).
Если принять степень консолидации, соответствующую полной стабилизированной осадке, за единицу и обозначить долю от полного уплотнения (т. е. степень консолидации для любого времени) через U, то ее значение найдем как отношение площади эпюры давлений в скелете грунта для времени t к площади полной (стабилизированной) эпюры давлений (при t=∞).
Высказанное положение математически можно записать в следующем виде:
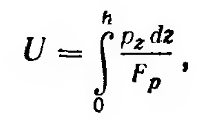
где Fp — плошадь полной стабилизированной эпюры уплотняющих давлений (в рассматриваемом случае Fp=ph).
Преобразуем выражение (обозначив для рассматриваемого основного случая степень консолидации через Uо):
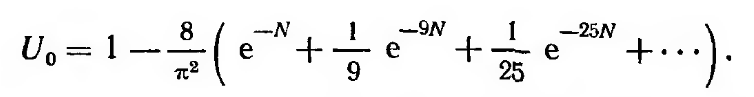
Так как e-N— правильная дробь, то для ряда практических случаев можно ограничиться первым членом ряда. Тогда будем иметь

Так как полному уплотнению соответствует полная стабилизированная осадка, а части уплотнения – осадка за время t, то степень консолидации (уплотнения) может быть выражена и следующим уравнением:

где st — осадка за данное время; s—полная стабилизированная осадка
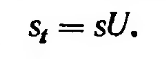
или получим для основного случая (равномерного распределения уплотняющих давлений по глубине) осадку для любого времени U
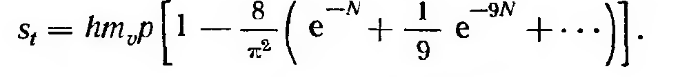
Дата добавления: 2015-01-29; просмотров: 1792; Мы поможем в написании вашей работы!; Нарушение авторских прав |