Интегрирование рациональных функций. Метод неопределенных коэффициентов

Определение 2.Рациональной будем называть функцию, которая представляется в виде:

,

где — многочлены степени соответственно.

Рациональная функция называется правильной (неправильной), если ( ).Каждую рациональную функцию (рациональную дробь) можно представить в виде суммы многочлена и правильной рациональной функции. Для этого в неправильной рациональной дроби надо разделить числитель на знаменатель.

Таким образом, для решения вопроса интегрирования рациональных функций достаточно детально рассмотреть интегрирование лишь правильных рациональных функций, потому что интегрирование многочленов не вызывает трудностей.

Определение 3. Простейшими рациональными функциями называются функции таких 4-х типов:

І. , ІІ. , ІІІ. , ІV.

где — действительные числа, а многочлен не имеет действительных корней, то есть . Каждая из этих функций является интегрированной:

І. ; (4.1)

ІІ. ; (4.2)

ІІІ.

; (4.3)

ІV. (4.4)

Первой из интегралов в правой части легко вычисляется:

.

Рассмотрим подробно вычисление второго интеграла:

Выведем рекурентную формулу для вычисления интегралов с помощью метода интегрирования по частям:

.

Последний интеграл можно преобразовать следующим образом:

.

Подставляя это выражение в предыдущее равенство, получим соотношение:

.

Разрешая последнее равенство относительно , получим:

(3.20)

Формула (3.20) является рекурентной формулой для вычисления интегралов вида . Она сводит вычисление к вычислению интеграла с предыдущим номером. Так — это табличный интеграл (берем одно из значений первообразных):

. (3.21)

Пользуясь (3.21), вычислим при помощи (3.20): , .

.

Для — :

=

,

и т.д. Таким образом можно вычислить интеграл для любого натурального показателя . Таким образом функции Іv-го типа также являются интегрированными. Из всего вышесказанного вытекает

Вывод: Каждая рациональная функция имеет первообразную.

Теорема 4. Каждая правильная рациональная дробь , может быть представлена в виде суммы конечного числа простейших рациональных функций, а потому имеет первообразную.

Разложение правильной дроби на простейшие дроби связано с разложением знаменателя на простые множители. Как известно из алгебры, каждый многочлен с действительными коэффициентами раскладывается на действительные множители типа , при этом предполагается, что квадратичные множители не имеют действительных корней, а потому не раскладываются на действительные линейные множители. Объединяя одинаковые множители, если такие есть, и предполагая для упрощения старший коэффициент равным единице, можно схематично записать разложение этого многочлена в виде:

,

где — натуральные числа.

Если при разложении на множители знаменателя дроби множитель входит в лишь в первой степени, то ему при разложении на простейшие будет отвечать одна дробь —

.

Если среди множителей присутствует , , то при разложении ему будет отвечать сумма простейших дробей:

,

где — вещественные постоянные.

Квадратичному множителю в разложении поставим в соответствие при разложении на простейшие одну дробь вида ІІІ

,

если входит в в первой степени, и сумму из простейших дробей

,

если этот множитель входит с показателем . Тут , — действительные постоянные.

Пример. Разложить на сумму простейших рациональных функций дробь

.

Знаменатель дроби уже разложен на простые множители: . Множителю будет отвечать сумма из 3-х простейших дробей, поскольку показатель степени при равен 3:

,

множителю — сумма из 2-х простейших дробей, поскольку показатель степени при равен 2:

,

множителю — сумма из 3-х простейших дробей, поскольку показатель степени при равен 3:

.

Таким образом:

,

где — действительные коэффициенты, которые пока являются неизвестными.

Для определения неизвестных коэффициентов надо:

1. Привести все полученные простейшие рациональные функции к общему знаменателю, сложить их;
2. Приравнять числители, которые являются многочленами, полученной после сложения простейших функций дроби и данной рациональной дроби. Два многочлена являются равными, когда у них совпадают коэффициенты при одинаковых степенях ;
3. Приравнять коэффициенты при одинаковых степенях многочленов в числителях. Результатом будет система линейных алгебраических уравнений относительно неизвестных коэффициентов разложения данной рациональной функции на сумму простейших;
4. Решить полученную систему.

Разложение правильной рациональной функции на сумму простейших дает возможность для ее интегрирования с помощью формул (4.1) — (4.4).

Пример. .

Подинтегральная функция является правильной рациональной дробью: степень многочлена числителя равняется 2, а знаменателя - 5. Для интегрирования сначала разложим подинтегральную функцию на сумму простейших дробей. Знаменатель содержит простые множители . Множителю отвечает сумма 2-х слагаемых (показатель степени при равен 2):

,

а множителю — одна дробь

.

Таким образом

. (4.5)

Найдем неизвестные коэффициенты . Для этого приведем все дроби в правой части к общему знаменателю:

,

тогда равенство (4.5) будет иметь вид:

.

Из равенства числителей

вытекает равенство коэффициентов многочленов при одинаковых степенях :

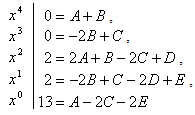
Откуда

.

Таким образом:

. (4.6)

Пользуясь формулой (4.6), проинтегрируем данную рациональную функцию:

.

С помощью (4.1) - (4.4) получим:

.

Вопросы

1. Какая функция называется первообразной функцией для функции в интервале ?

2. Сколько первообразных вообще может иметь функция ?

3. Чем отличаются между собой первообразные одной функции?

4. Что такое неопределенный интеграл для функции ?

5. Свойства неопределенного интеграла?

6. Каждая ли функция имеет первообразную?

7. Какой должна быть функция , чтобы для нее обязательно существовала первообразная?

8. Основная теорема интегрального исчисления.

9. Какой должна быть функция , чтобы для нее обязательно не существовала первообразная?

10. В чем состоит метод замены переменной для вычисления неопределенного интеграла? Привести примеры использования этого метода для вычисления интегралов.

11. В чем состоит метод интегрирования по частям для вычисления неопределенного интеграла? Привести примеры использования этого метода для вычисления интегралов.

12. Какая функция называется рациональной? Привести примеры рациональных функций. Когда рациональная функция называется правильной (неправильной)?

13. Какие функции называются простейшими рациональными функциями?

14. Что можно сказать об интегрированности простейших рациональных функций?

15. Что можно сказать об интегрированности любой рациональной функции?

16. Как происходит разложение правильной дроби на простейшие дроби?

17. Метод неопределенных коэффициентов.