Обработка результатов многократных измерений

Многократные измерения одной и той же величины постоянного размера производятся при повышенных требованиях к точности измерений. Результат многократных измерений описывается выражением:

. (7)

Как и результат однократного измерения, он является случайным значением измеряемой величины, но его дисперсия в n раз меньше дисперсии результата однократного измерения:

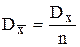, соответственно (8)

То есть точность определения значения измеряемой величины повышается в раз.

Результат многократных измерений записывается в форме доверительного интервала

, (9)

где величина t находится в зависимости от заданной доверительной вероятности.

При проведении многократных измерений некоторые результаты могут содержатьгрубые погрешности, то есть погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента (измерения). Очевидно, что наиболее подозрительными являются минимальное и максимальное показания. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами проверки статистических гипотез.

Проверяемая гипотеза состоит в утверждении, что результат х_i не содержит грубой погрешности. Для проверки этой гипотезы при небольшом числе наблюдений используют распределения следующих величин:

, (10)

. (11)

Эти функции совпадают между собой, и для нормального распределения результатов измерения они протабулированы. По табл.1 приложения по заданной доверительной вероятности Р и количестве измерений в серии n находят табличное (предельно допустимое) значение n_т; его сравнивают с расчетным значением n_р. Если выполняется условие n_р < n_т , то гипотеза об отсутствии грубой погрешности принимается с вероятностью Р.

После того, как грубые погрешности (промахи) исключены из результатов измерения, необходимо снова определить оценки числовых характеристик и вновь убедиться в отсутствии грубых погрешностей.

2.3.Однородные и неоднородныесерии измерений

Часто измерительная процедура бывает организована таким образом, что с помощью каждого средства измерений получают ряд значений отсчета - серию измерений.При этом могут получаться как однородные, так и неоднородные серии.

Однородными сериями измерений называются такие, у которых распределение вероятности результатов измерений подчиняется одному закону. На практике однородными считают такие серии измерений, у которых числовые характеристики законов распределения вероятности (ЗРВ) и отличаются случайным образом. Если хотя бы одна из этих числовых характеристик отличается от характеристик других серий неслучайно, то эти серии считаются неоднородными.

При неслучайном различии средних 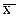результаты серий измерений не подлежат совместной обработке, так как результаты измерений не сходятся. Обычно причиной расхождения является неисключенная систематическая погрешность или резко изменившиеся условия измерений. Однако поскольку при выполнении данной лабораторной работы ни одно из этих обстоятельств не возникает, то выполнять проверку сходимости средних в данном случае не предусматривается.

При неслучайном различии дисперсий серии измерений являются неравноточными (неравнорассеянными).

Результаты равноточных и неравноточных серий измерений подлежат совместной обработке, но по различным методикам. Поэтому перед тем, как приступить к обработке результатов нескольких серий измерений, необходимо произвести проверку их равноточности.

Чаще всего для проверки равноточности дисперсий используют критерий Фишера.

Критерий Фишера определяется по формуле:

, (12)

где F_р - расчетное значение критерия Фишера,

- наибольшая и наименьшая дисперсии из всех серий.

Если выполняется условие

, (13)

то дисперсии - однородны. Следовательно, остальные дисперсии однородны тем более.

Критическое (табличное) значение F-критерия F_T выбирается по табл. 3 приложения в зависимости от доверительной вероятности Р и числа степеней свободы k₁ = n₁ - 1, k₂ = n₂ – 1, где k₁ и k₂ - числа степеней свободы для наибольшей и наименьшей дисперсий соответственно.