Дифференциальное уравнение

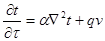
где t – температура тела, τ – время, q – плотность теплового потока,

где – оператор Лапласа, α – коэффициент температуропроводности.

Дифференциальное уравнение описывает в самом общем виде все без исключения задачи теплопроводности. Для выделения конкретной задачи необходимы дополнительные данные, которые называются краевыми условиями или условиями однозначности. Существуют различные условия однозначности: геометрические – характеризующие форму и размеры тела, в котором протекает процесс теплопроводности; физические – характеризующие физические свойства тела; временные – характеризующие распределение температуры тела в начальный момент времени, граничные – характеризующие взаимодействие тела с окружающей средой.

Граничные условия в свою очередь бывают трех родов:

1) при первом задается распределении температуры на поверхности тела в функции времени;

2) при втором – плотность теплового потока для всей поверхности тела в функции времени;

3) при третьем – температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой – закон Ньютона – Рихмана

dQ_τ = α (t_o – t_ж) dFdτ

где t_o – температура поверхности тела; α – коэффициент пропорциональности, называемый коэффициентом теплоотдачи,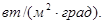

Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности за единицу времени при разности температур между поверхностью тела и окружающей средой в 1 град. Этот коэффициент учитывает все особенности явлений теплообмена, происходящего между поверхностью тела и окружающей средой.