
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
И граничных условиях первого рода
Плоская стенка. Рассмотрим однородную плоскую стенку толщиной δ (рисунок )
На наружных поверхностях стенки поддерживаются постоянные температуры tc1 и tc2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме (  ) и отсутствии внутренних источников теплоты (qv = 0) дифференциальное уравнение теплопроводности примет вид
) и отсутствии внутренних источников теплоты (qv = 0) дифференциальное уравнение теплопроводности примет вид

Общее количество теплоты, которое передается через поверхность стенки F за время τ:

Отношение  называют тепловой проводимостью стенки, обратную ему величину
называют тепловой проводимостью стенки, обратную ему величину  – термическим сопротивлением теплопроводности. В связи с зависимостью величины λ от температуры в уравнениях необходимо подставить коэффициент теплопроводности λср, взятый при средней температуре стенки
– термическим сопротивлением теплопроводности. В связи с зависимостью величины λ от температуры в уравнениях необходимо подставить коэффициент теплопроводности λср, взятый при средней температуре стенки  .
.
Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n однородных слоев (рисунок ).
Коэффициент теплопроводности каждого слоя равен соответственно λ1, λ2, … λn, толщины слоев – δ1, δ2, … δn . Принимаем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях двух слоев одинакова. При стационарном режиме количество подведенной и отведенной от стенки теплоты должно быть одинаково. Отсюда вытекает равенство тепловых потоков, проходящих через каждый слой стенки.
На основании запишем для каждого слоя:


………………

Из этих уравнений определяем температурные напоры:


……………….

Складывая левые и правые части уравнений, находим

Отсюда плотность теплового потока

где i – номер слоя. Величина  называется полным термическим сопротивлением теплопроводности многослойной стенки. Графически распределение температур по сечению многослойной стенки представляется ломаной линией, температуры на границе соприкосновения слоев можно определять уравнением
называется полным термическим сопротивлением теплопроводности многослойной стенки. Графически распределение температур по сечению многослойной стенки представляется ломаной линией, температуры на границе соприкосновения слоев можно определять уравнением

Цилиндрическая стенка. Рассмотрим стационарный процесс теплопроводности через однородную цилиндрическую стенку (трубу) длиной l с внутренним радиусом r1 и наружным r2 (рисунок ).
Коэффициент теплопроводности материала стенки λ является постоянной величиной. На поверхности стенки заданы постоянные температуры tс1 и tс2.
В этом случае изотермические поверхности будут цилиндрическими, а температурное поле одномерным, т.е. t = f (r), где r – текущая координата цилиндрической системы.
Уравнение распределения температур по толщине стенки и количество передаваемой через нее теплоты можно получить путем интегрирования уравнения:

выразив оператор Лапласа в цилиндрической системе координат. Для упрощения математических преобразований применим иной метод решения этой задачи. Выделим внутри стенки кольцевой слой радиусом r и толщиной dr. Проходящий через этот слой тепловой поток
 .
.
Разделив переменные, получаем
 .
.
Интегрирование этого уравнения дает

Для определения постоянной С воспользуемся граничными условиями первого рода: при r = r1 t = tс1; r = r2 t = tс2.
Подставляем эти граничные условия в уравнение:


Вычитаем из первого уравнения второе:

Так как площади внутренней и внешней поверхностей трубы различны, различными оказываются и соответствующие плотности тепловых потоков. В технических расчетах тепловой поток относится к единице длины цилиндрической стенки, т.е. линейная плотность теплового потока

Уравнение температурной кривой внутри однородной цилиндрической стенки получаем из уравнения путем замены tс2 на t и d2 на d:

В случае многослойной цилиндрической стенки линейная плотность теплового потока ql будет одинаковой для каждого слоя. Воспользовавшись методом решения задачи теплопроводности через многослойную плоскую стенку, находим

Величина  называется линейным термическим сопротивлением теплопроводности отдельного слоя, а
называется линейным термическим сопротивлением теплопроводности отдельного слоя, а  – суммарным линейным термическим сопротивлением теплопроводности цилиндрической стенки. Температура на границе любых слоев определится по уравнению
– суммарным линейным термическим сопротивлением теплопроводности цилиндрической стенки. Температура на границе любых слоев определится по уравнению
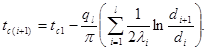
Дата добавления: 2015-01-29; просмотров: 266; Мы поможем в написании вашей работы!; Нарушение авторских прав |