Слабые электролиты. Константа диссоциации

Диссоциация слабых электролитов протекает обратимо и к нему можно применить закон действующих масс. Так, для процесса диссоциации уксусной кислоты

СH₃COOH⟺CH₃COO^‒ + H⁺

константа равновесия К_С будет равна

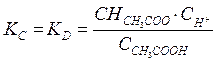(4.14)

Константа равновесия процесса диссоциации и называется константой диссоциации k_D.

Константа диссоциации зависит от природы диссоциирующего вещества, растворителя и не зависит от концентрации. С увеличением температуры К_D уменьшается.

Согласно принципу Ле Шателье температурная зависимость k_D указывает на то, что процесс диссоциации является экзотермическим.

Чем меньше k_D, тем слабее диссоциирует электролит и тем устойчивее его молекулы. Сильные электролиты диссоциируют полностью, поэтому k_D для них теряет смысл. Для сильных электролитов К_D ³ 10^-2, для слабых К_D £ 10^-5.

Количество ионов в растворах сильных электролитов больше чем в растворах слабых той же концентрации.

Константа диссоциации указывает на прочность молекул слабых электролитов в данном растворе. Чем меньше константа диссоциации в данном растворителе, тем слабее диссоциирует электролит и тем, следовательно, устойчивее его молекулы. Учитывая, что степень диссоциации в отличие от константы диссоциации изменяется с концентрацией раствора, необходимо выяснить связь между степенью диссоциации электролита и концентрацией его в растворе. Для этого рассмотрим реакцию диссоциации:

A_mB_n⟺mA⁺+nB^-,

где m, n-стехиометрические коэффициенты (индексы).

Если обозначить концентрации катионов А⁺ через С_A⁺ , а анионов В^- - через С_B^- концентрацию недиссоциированного остатка A_mВ_n - через С_AmВn , то, применяя к реакции закон действующих масс, получим константу диссоциации электролита

(4.15)

Если исходная концентрация или брутто-концентрация соединения A_mВ_n, равна С₀, то, очевидно

С_A⁺ = m α С₀ (4.16)

С_B^- = n α С₀ (4.17)

С_AmВn = С₀ (1 – α ) (4.18)

Подставляя значения С_A⁺, С_B^- и С_AmВn из (4.16) - (4.18) в уравнение (4.15), будем иметь

(4.19)

или

(4.20)

Для бинарного электролита АВ ( m =1, n =1) уравнение примет вид

(4.21)

Это обобщенное уравнение закона разведения Оствальда.