Многоэлектронные атомы

В атоме водорода электрон находится в силовом поле, которое создается только ядром. В многоэлектронных атомах на каждый электрон действует не только ядро, но и все остальные электроны. При этом электронные облака отдельных электронов как бы сливаются в одно общее многоэлектронное облако. Точное решение уравнения Шредингера для таких сложных систем связано с большими затруднениями и, как правило, недостижимо. Поэтому состояние электронов в сложных атомах и в молекулах определяют путем приближенного решения уравнения Шредингера.

Общим для всех приближенных методов решения этого уравнения является так называемое одноэлектронное приближение, т.е. предположение, что волновая функция многоэлектронной системы может быть представлена в виде суммы волновых функций отдельных электронов. Тогда уравнение Шредингера может решаться отдельно для каждого находящегося в атоме электрона, состояние которого, как и в атоме водорода, будет определяться значениями квантовых чисел n, l, m и s. Однако и при этом упрощении решение уравнения Шредингера для многоэлектронных атомов и молекул представляет весьма сложную задачу и требует большого объема трудоемких вычислений. В последние годы подобные вычисления выполняются, как правило, с помощью быстродействующих электронных вычислительных машин, что позволило произвести необходимые расчеты для атомов всех элементов и для многих молекул.

Исследование спектров многоэлектронных атомов показало, что здесь энергетическое состояние электронов зависит не только от главного квантового числа n, но и от орбитального квантового числа l. Это связано с тем, что электрон в атоме не только притягивается ядром, но и испытывает отталкивание со стороны электронов, расположенных между данным электроном и ядром. Внутренние электронные слои как бы образуют своеобразный экран, ослабляющий притяжение электрона к ядру, или, как принято говорить, экранируют внешний электрон от ядерного заряда. При этом для электронов, различающихся значением орбитального квантового числа l, экранирование оказывается неодинаковым.

Так, в атоме натрия (порядковый номер Z=11) ближайшие к ядру К- шли L-слои заняты десятью электронами; одиннадцатый электрон принадлежит к M-слою (n = 3). На рис. 1 кривая 1 изображает радиальное распределение вероятности для суммарного электронного облака десяти «внутренних» электронов атома натрия: ближайший к ядру максимум электронной плотности соответствует К-слою, второй максимум- L-слою. Преобладающая часть внешнего электронного облака атома натрия расположена вне области, занятой внутренними электронами, и потому сильно экранируется. Однако часть этого электронного облака проникает в пространство, занятое внутренними электронами, и потому экранируется слабее.

Рисунок 1 - График радиального распределения в атоме натрия: 1 – для десяти электронов K и L-слоев; 2 – для 3S-электрона; 3 – для 3Р-электрона

Какое же из возможных состояний внешнего электрона атома натрия - 3s, Зр или 3d- отвечает более слабому экранированию и, следовательно, более сильному притяжению к ядру и более низ-кон энергии электрона? Как показывает рис. 2, электронное облако Зs-электрона в большей степени проникает в область, занятую электронами K- и L-слоев, и потому экранируется слабее, чем электронное облако Зр-электрона. Следовательно, электрон в состоянии 3s будет сильнее притягиваться к ядру и обладать меньшей энергией, чем электрон в состоянии Зр. Электронное облако Зd-орбитали практически полностью находится вне области, занятой внутренними электронами, экранируется в наибольшей степени и наиболее слабо притягивается к ядру. Именно поэтому устойчивое состояние атома натрия соответствует размещению внешнего электрона на орбитали 3s.

Таким образом, в многоэлектронных атомах энергия электрона зависит не только от главного, но и от орбитального квантового числа. Главное квантовое число определяет здесь лишь некоторую энергетическую зону, в пределах которой точное значение энергии электрона определяется величиной l. В результате возрастание энергии по энергетическим подуровням происходит примерно в следующем порядке.

В многоэлектронных атомах вследствие взаимного электростатического отталкивания электронов существенно уменьшается прочность их связи с ядром. Например, энергия отрыва электрона от иона Не⁺ равна 54,4 эВ, в нейтральном атоме Не она значительно меньше - 24,6 эВ. Для более тяжелых атомов связь внешних электронов с ядром еще слабее.

Важную роль в многоэлектронных атомах играет специфическое обменное взаимодействие, связанное с неразличимостью электронов, и тот факт, что электроны подчиняются Паули принципу, согласно которому, в каждом квантовом состоянии, характеризуемом четырьмя квантовыми числами, не может находиться более одного электрона. Для многоэлектронного атома имеет смысл говорить только о квантовых состояниях всего атома в целом.

Однако приближенно, в так называемом одноэлектронном приближении, можно рассматривать квантовые состояния отдельных электронов и характеризовать каждое одноэлектронное состояние (определенную орбиталъ, описываемую соответствующей функцией) совокупностью четырех квантовых чисел n, l, m_l и m_s. Совокупность 2(2l+ 1) электронов в состоянии с данными n и l образует электронную оболочку (называемую также подуровнем, подоболочкой); если все эти состояния заняты электронами, оболочка называется заполненной (замкнутой).

106 Эффективный заряд ядра, электронные конфигурации атомов и ионов.

В зависимости от преследуемой цели практикуются различные способы записи электронных конфигураций атомов и ионов.

Электронные оболочки. Наиболее простой способ – запись по электронным оболочкам. При этом указываются заряд ядра и количество электронов на каждый электронной оболочке по мере увеличения её номера. Например, для атома азота и его иона N⁺ электронная конфигурация по оболочкам выглядит так

_{\ \ \ \}

₇N (7ē) 2 5 ₇N⁺ (6ē) 2 4

/ / / /

Как было показано ранее, максимальное число электронов по n электронной оболочке равно 2n². Тогда на первой оболочке может разместиться максимум два электрона, а на второй не более 8. Однако, у атома азота всего семь электронов (общее число электронов в атоме равно заряду ядра), поэтому на второй оболочке разместятся остальные 7 – 2 = 5 электронов. В положительно заряженном ионе азота заряд ядра превышает суммарный заряд электронов на +1, поэтому число электронов в данном ионе на один меньше, чем в атоме. При этом удаляют электрон с внешней электронной оболочки.

Электронные оболочки и подоболочки. Этот метод записи электронных конфигураций используют наиболее часто. Номер электронной оболочки (главное квантовое число) указывают цифрой, а тип подоболочки (орбитальное квантовое число) – буквой s-, p-, d- или f-. Количество электронов указывается цифрой справа вверху у символа подоболочки. Для атома и иона азота данная запись имеет следующий вид:

₇N 1s²2s²2p³ ₇N⁺ 1s²2s²2p².

В соответствии с максимальной возможной заселенностью s-подоболочек, равной 2, первые четыре электрона полностью заполняют первую и вторую подоболочки. Оставшиеся электроны размещаются на р-подоболочке.

Электронные оболочки, подоболочки и заселенность орбиталей. При обсуждении валентности атомов и ионов, изучении природы химической связи, исследовании магнитных и других свойств атомов, молекул или их ионов применяют способ записи по электронным оболочкам, подоболочкам с указанием заселенности орбиталей электронами. Опираясь на запись электронных конфигураций по оболочкам и подоболочкам, в данном способе учитывают максимальное количество атомных орбиталей (АО) электронной подоболочки и производят размещение электронов среди них в соответствии с правилом Фридриха Хунда (Гунда) (1896-1989): электроны в атоме размещаются таким образом, чтобы занять возможно большее число атомных орбиталей, чтобы абсолютное значение суммарного спина было максимальным.

Три электрона на р-подуровне можно разместить по разному

или

-↑- -↑- -↑- -↑- -↓- -↑- -↑↓- -↑- ---

Однако верным будет первый способ размещения, отвечающий правилу Хунда.

Существует другая форма записи графических электронных формул в виде ячеек.

Каждая такая ячейка обозначается: клетка – орбиталь, стрелка – электрон, направление стрелки – направление спина, свободная клетка – свободная орбиталь, которую может занимать электрон при возбуждении.

Согласно принципу Паули, в ячейке может быть один или два электрона (если два электрона, то они спарены). В таком случае, например, схема распределения электронов по квантовым ячейкам в атоме углерода следующая:

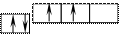
n =2 p_x p_y p_z

₆C 1s²2s²2p_x¹2p_y¹

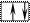n = 1

Орбитали р-подуровня заполняются так: сначала по одному электрону с одинаковыми спинами, а затем по второму электрону с противоположными спинами. Поскольку на 2р-подуровне три орбитали с одинаковой энергией, то каждый из двух 2р-электро-нов занимает по одной орбитали (например, р_х и р_у). Одна орбиталь остается свободной (р_z). Таким образом, у атома углерода два неспаренных электрона. Справа от схемы в электронной формуле дана более подробная запись с указанием расположения электронов на р_х и р_у-орбиталях.

В атоме азота все три 2р-орбитали заняты электронами

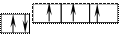
n =2 p_x p_y p_z

₇N 1s²2s²2p_x¹2p_y¹2p_z¹

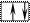n = 1

s

Согласно принципу наименьшей энергии во многих случаях электрону энергетически выгоднее занять подуровень «вышележащего» уровня, хотя подуровень «нижележащего» уровня не заполнен. Именно поэтому у элементов четвертого периода периодической системы элементов Д.И. Менделеева, сначала заполняется подуровень 4s- и лишь после этого подуровень 3d-. Элементы, у которых идет заполнение d- и f-подуровней, обычно называют переходными.

Принцип Паули.

В 1925 г. Паули установил квантово - механический принцип (принцип запрета Паули).

В любом атоме не может быть двух электронов, находящихся в одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел: n, , m, ms.

Например, на энергетическом уровне может находиться не более двух электронов, но с противоположным направлением спинов.

Принцип Паули дал возможность теоретически обосновать периодическую систему элементов Менделеева, создать квантовые статистики, современную теорию твердых тел и др.