Принцип разомкнутого управления. Принцип компенсации. Принцип обратной связи.

Принцип разомкнутого управления

Функциональная схема СУ, реализующая принцип разомкнутого управления, представлена на рис. 9.

F(t)

Y_зад(t) U(t) Y(t)

Рис. 9. Принцип разомкнутого управления

Здесь управляющее воздействие U(t) вырабатывается только на основе заданного алгоритма функционирования и не контролируется другими факторами - возмущениями f(t) и выходными координатами Y(t). Близость Y(t) и Yзад(t) обеспечивается только конструкцией и совокупностью физических закономерностей, действующих во всех элементах. Схема системы имеет вид разомкнутой цепи.

Общих правил построения разомкнутых систем немного, они зависят от частных свойств конкретных элементов системы.

Главная особенность принципа разомкнутого управления - процесс работы не зависит от результата.

Принцип компенсации

Функциональная схема системы управления, иллюстрирующая принцип компенсации (принцип управления по возмущению), представлена на рис. 10.

	Компенсатор

f(t)

U₂(t)

Рис. 10. Принцип компенсации

Для обеспечения требуемой точности выполнения алгоритма функционирования вводятся коррективы, зависящие от возмущения:

(7.1)

Такая схема может быть реализована, если существует возможность получения информации о возмущающем воздействии f(t).

Принцип компенсации по-другому называется принципом управления по возмущению. В 1940-1950-х гг. советские ученые Г. В. Щипанов, В. С. Кулебакин, Б. Н. Петров показали, как нужно строить системы управления с компенсацией возмущений. В теорию управления был введен принцип инвариантности.

Принцип обратной связи

Функциональная схема, иллюстрирующая принцип обратной связи (принцип управления по отклонению), приведена на рис. 11.

f(t)

Y_зад(t) U₁(t) U(t) Y(t)

-

Рис. 11. Принцип обратной связи

Принцип управления с использованием информации о реакции объекта на управляющее действие называется принципом обратной связи.

Схема рис. 11 имеет вид замкнутой цепи. В ней коррективы в управляющее воздействие вводятся по фактическому значению координат в объекте.

В системах управления широко распространен частный вид замкнутых систем, в которых управление осуществляется по отклонениям значений координат Y(t) от их заданных значений Y_3aд(t)

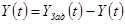(7.2)

В этом случае схема системы управления имеет следующий вид:

F(t)

Y_зад(t) ∆Y(t) U₁(t) U(t) Y(t)

Рис. 12. Принцип управления по отклонению

Величина ∆Y(t) называется отклонением, или ошибкой управления. Управление в функции отклонения называют регулированием, а управляющее устройство в таком случае называется автоматическим регулятором.

На практике принцип обратной связи в системах управления применяется одновременно с принципом компенсации.